
【題目】共有編號分別為1,2,3,4,5的五個座位,在甲同學(xué)不坐2號座位,乙同學(xué)不坐5號座位的條件下,甲、乙兩位同學(xué)的座位號相加是偶數(shù)的概率為( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】A
【解析】
先求出事件:甲同學(xué)不坐2號座位,乙同學(xué)不坐5號座位的基本事件的總數(shù),再求得事件:甲、乙兩位同學(xué)的座位號相加是偶數(shù)包含事件的個數(shù),然后代入古典概型的概率公式即可。
設(shè)甲同學(xué)的座位號為a,乙同學(xué)的座位號b,則事件:甲同學(xué)不坐2號座位,乙同學(xué)不坐5號座位包含的基本事件為(1,2)、(1,3)、(1,4)、(3、1)、(3,2)、(3,4)、(4,1)、(4,2)、(4,3)、(5,1)(5,2)、(5,3)、(5,4),共13種情況。事件:甲、乙兩位同學(xué)的座位號相加是偶數(shù)包含(1,3)、(3、1)、(4,2)、(5,1)、(5,3)共5種情況,所以該事件發(fā)生的該![]() ,選A。
,選A。


科目:高中數(shù)學(xué) 來源: 題型:
【題目】自從新型冠狀病毒爆發(fā)以來,全國范圍內(nèi)采取了積極的措施進行防控,并及時通報各項數(shù)據(jù)以便公眾了解情況,做好防護.以下是湖南省2020年1月23日-31日這9天的新增確診人數(shù).
日期 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 |
時間 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
新增確診人數(shù) | 15 | 19 | 26 | 31 | 43 | 78 | 56 | 55 | 57 |
經(jīng)過醫(yī)學(xué)研究,發(fā)現(xiàn)新型冠狀病毒極易傳染,一個病毒的攜帶者在病情發(fā)作之前通常有長達14天的潛伏期,這個期間如果不采取防護措施,則感染者與一位健康者接觸時間超過15秒,就有可能傳染病毒.
(1)將1月23日作為第1天,連續(xù)9天的時間作為變量x,每天新增確診人數(shù)作為變量y,通過回歸分析,得到模型![]() 用于對疫情進行分析.對上表的數(shù)據(jù)作初步處理,得到下面的一些統(tǒng)計量的值(部分?jǐn)?shù)據(jù)已作近似處理):
用于對疫情進行分析.對上表的數(shù)據(jù)作初步處理,得到下面的一些統(tǒng)計量的值(部分?jǐn)?shù)據(jù)已作近似處理):![]() ,
,![]() .根據(jù)相關(guān)數(shù)據(jù),求該模型的回歸方程(結(jié)果精確到0.1),并依據(jù)該模型預(yù)測第10天新增確診人數(shù).
.根據(jù)相關(guān)數(shù)據(jù),求該模型的回歸方程(結(jié)果精確到0.1),并依據(jù)該模型預(yù)測第10天新增確診人數(shù).
(2)如果一位新型冠狀病毒的感染者傳染給他人的概率為0.3,在一次12人的家庭聚餐中,只有一位感染者參加了聚餐,記余下的人員中被感染的人數(shù)為![]() ,求
,求![]() 最有可能(即概率最大)的值是多少.
最有可能(即概率最大)的值是多少.
附:對于一組數(shù)據(jù)![]() ,
,![]() …,
…,![]() ,其回歸直線
,其回歸直線![]() 的斜率和截距的最小二乘估計分別為
的斜率和截距的最小二乘估計分別為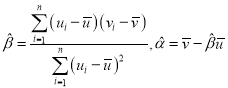 .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】
甲、乙兩個籃球運動員互不影響地在同一位置投球,命中率分別為![]() 與
與![]() ,且乙投球2次均未命中的概率為
,且乙投球2次均未命中的概率為![]() .
.
(Ⅰ)求乙投球的命中率![]() ;
;
(Ⅱ)若甲投球1次,乙投球2次,兩人共命中的次數(shù)記為![]() ,求
,求![]() 的分布列和數(shù)學(xué)期望.
的分布列和數(shù)學(xué)期望.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知圓![]() 的圓心
的圓心![]() 的坐標(biāo)為
的坐標(biāo)為![]() ,且圓
,且圓![]() 與直線
與直線![]() :
:![]() 相切,過點
相切,過點![]() 的動直線
的動直線![]() 與圓
與圓![]() 相交于
相交于![]() ,
,![]() 兩點,直線
兩點,直線![]() 與直線
與直線![]() 的交點為
的交點為![]() .
.
(1)求圓![]() 的標(biāo)準(zhǔn)方程;
的標(biāo)準(zhǔn)方程;
(2)求![]() 的最小值;
的最小值;
(3)問:![]() 是否是定值?若是,求出這個定值;若不是,請說明理由.
是否是定值?若是,求出這個定值;若不是,請說明理由.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】某音樂院校舉行“校園之星”評選活動,評委由本校全體學(xué)生組成,對![]() 兩位選手,隨機調(diào)查了
兩位選手,隨機調(diào)查了![]() 個學(xué)生的評分,得到下面的莖葉圖:
個學(xué)生的評分,得到下面的莖葉圖:
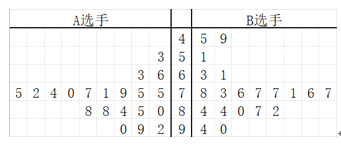
![]() 通過莖葉圖比較
通過莖葉圖比較![]() 兩位選手所得分?jǐn)?shù)的平均值及分散程度(不要求計算出具體值,得出結(jié)論即可);
兩位選手所得分?jǐn)?shù)的平均值及分散程度(不要求計算出具體值,得出結(jié)論即可);
![]() 校方將會根據(jù)評分記過對參賽選手進行三向分流:
校方將會根據(jù)評分記過對參賽選手進行三向分流:
所得分?jǐn)?shù) | 低于 |
| 不低于 |
分流方向 | 淘汰出局 | 復(fù)賽待選 | 直接晉級 |
記事件![]() “
“![]() 獲得的分流等級高于
獲得的分流等級高于![]() ”,根據(jù)所給數(shù)據(jù),以事件發(fā)生的頻率作為相應(yīng)事件發(fā)生的概率,求事件
”,根據(jù)所給數(shù)據(jù),以事件發(fā)生的頻率作為相應(yīng)事件發(fā)生的概率,求事件![]() 發(fā)生的概率.
發(fā)生的概率.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】某企業(yè)新研發(fā)了一種產(chǎn)品,產(chǎn)品的成本由原料成本及非原料成本組成.每件產(chǎn)品的非原料成本![]() (元)與生產(chǎn)該產(chǎn)品的數(shù)量
(元)與生產(chǎn)該產(chǎn)品的數(shù)量![]() (千件)有關(guān),經(jīng)統(tǒng)計得到如下數(shù)據(jù):
(千件)有關(guān),經(jīng)統(tǒng)計得到如下數(shù)據(jù):
![]()
根據(jù)以上數(shù)據(jù),繪制了散點圖.
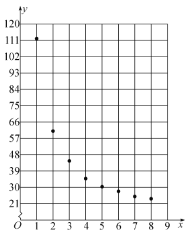
觀察散點圖,兩個變量不具有線性相關(guān)關(guān)系,現(xiàn)考慮用反比例函數(shù)模型![]() 和指數(shù)函數(shù)模型
和指數(shù)函數(shù)模型![]() 分別對兩個變量的關(guān)系進行擬合.已求得用指數(shù)函數(shù)模型擬合的回歸方程為
分別對兩個變量的關(guān)系進行擬合.已求得用指數(shù)函數(shù)模型擬合的回歸方程為![]() ,
,![]() 與
與![]() 的相關(guān)系數(shù)
的相關(guān)系數(shù)![]() .參考數(shù)據(jù)(其中
.參考數(shù)據(jù)(其中![]() ):
):

(1)用反比例函數(shù)模型求![]() 關(guān)于
關(guān)于![]() 的回歸方程;
的回歸方程;
(2)用相關(guān)系數(shù)判斷上述兩個模型哪一個擬合效果更好(精確到0.01),并用其估計產(chǎn)量為10千件時每件產(chǎn)品的非原料成本;
(3)該企業(yè)采取訂單生產(chǎn)模式(根據(jù)訂單數(shù)量進行生產(chǎn),即產(chǎn)品全部售出).根據(jù)市場調(diào)研數(shù)據(jù),若該產(chǎn)品單價定為100元,則簽訂9千件訂單的概率為0.8,簽訂10千件訂單的概率為0.2;若單價定為90元,則簽訂10千件訂單的概率為0.3,簽訂11千件訂單的概率為0.7.已知每件產(chǎn)品的原料成本為10元,根據(jù)(2)的結(jié)果,企業(yè)要想獲得更高利潤,產(chǎn)品單價應(yīng)選擇100元還是90元,請說明理由.
參考公式:對于一組數(shù)據(jù)![]() ,
,![]() ,…,
,…,![]() ,其回歸直線
,其回歸直線![]() 的斜率和截距的最小二乘估計分別為:
的斜率和截距的最小二乘估計分別為: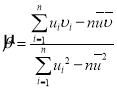 ,
,![]() ,相關(guān)系數(shù)
,相關(guān)系數(shù)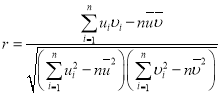 .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】某企業(yè)新研發(fā)了一種產(chǎn)品,產(chǎn)品的成本由原料成本及非原料成本組成.每件產(chǎn)品的非原料成本![]() (元)與生產(chǎn)該產(chǎn)品的數(shù)量
(元)與生產(chǎn)該產(chǎn)品的數(shù)量![]() (千件)有關(guān),經(jīng)統(tǒng)計得到如下數(shù)據(jù):
(千件)有關(guān),經(jīng)統(tǒng)計得到如下數(shù)據(jù):
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 112 | 61 | 44.5 | 35 | 30.5 | 28 | 25 | 24 |
根據(jù)以上數(shù)據(jù),繪制了散點圖.
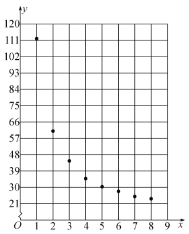
觀察散點圖,兩個變量不具有線性相關(guān)關(guān)系,現(xiàn)考慮用反比例函數(shù)模型![]() 和指數(shù)函數(shù)模型
和指數(shù)函數(shù)模型![]() 分別對兩個變量的關(guān)系進行擬合.已求得用指數(shù)函數(shù)模型擬合的回歸方程為
分別對兩個變量的關(guān)系進行擬合.已求得用指數(shù)函數(shù)模型擬合的回歸方程為![]() ,
,![]() 與
與![]() 的相關(guān)系數(shù)
的相關(guān)系數(shù)![]() .
.
參考數(shù)據(jù)(其中![]() ):
):
|
|
|
|
|
|
|
|
183.4 | 0.34 | 0.115 | 1.53 | 360 | 22385.5 | 61.4 | 0.135 |
(1)用反比例函數(shù)模型求![]() 關(guān)于
關(guān)于![]() 的回歸方程;
的回歸方程;
(2)用相關(guān)系數(shù)判斷上述兩個模型哪一個擬合效果更好(精確到0.01),并用其估計產(chǎn)量為10千件時每件產(chǎn)品的非原料成本;
(3)該企業(yè)采取訂單生產(chǎn)模式(根據(jù)訂單數(shù)量進行生產(chǎn),即產(chǎn)品全部售出).根據(jù)市場調(diào)研數(shù)據(jù),若該產(chǎn)品單價定為100元,則簽訂9千件訂單的概率為0.8,簽訂10千件訂單的概率為0.2;若單價定為90元,則簽訂10千件訂單的概率為0.3,簽訂11千件訂單的概率為0.7.已知每件產(chǎn)品的原料成本為10元,根據(jù)(2)的結(jié)果,企業(yè)要想獲得更高利潤,產(chǎn)品單價應(yīng)選擇100元還是90元,請說明理由.
參考公式:對于一組數(shù)據(jù)![]() ,
,![]() ,…,
,…,![]() ,其回歸直線
,其回歸直線![]() 的斜率和截距的最小二乘估計分別為:
的斜率和截距的最小二乘估計分別為: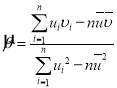 ,
,![]() ,相關(guān)系數(shù)
,相關(guān)系數(shù)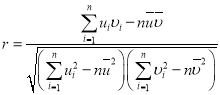 .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖1,在等腰梯形![]() 中,
中,![]() 分別為
分別為![]() 的中點.現(xiàn)分別沿
的中點.現(xiàn)分別沿![]() 將
將![]() 和
和![]() 折起,使得平面
折起,使得平面![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,連接
,連接![]() ,如圖2.
,如圖2.
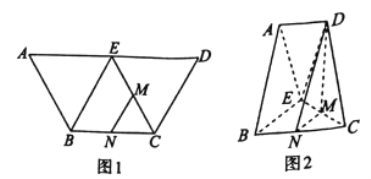
(1)求證:平面![]() 平面
平面![]() ;
;
(2)求多面體![]() 的體積.
的體積.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com