
【題目】已知橢圓![]() 上的點到兩個焦點的距離之和為
上的點到兩個焦點的距離之和為![]() ,短軸長為
,短軸長為![]() ,直線
,直線![]() 與橢圓C交于M、N兩點.
與橢圓C交于M、N兩點.
(1)求橢圓C的方程;
(2)若直線![]() 與圓
與圓![]() 相切,證明:
相切,證明:![]() 為定值
為定值
【答案】(1)![]() (2)詳見解析
(2)詳見解析
【解析】
(1)根據橢圓的有關知識可得![]() ,從而可得橢圓的方程;
,從而可得橢圓的方程;
(2)分直線的斜率存在與否兩種情況求解.①當![]() 的斜率不存在時,其方程為
的斜率不存在時,其方程為![]() ,可得
,可得![]() 、
、![]() 的坐標,由向量的數量積可得
的坐標,由向量的數量積可得![]() ;②當
;②當![]() 的斜率存在時,設其方程為
的斜率存在時,設其方程為![]() ,由直線與圓相切得
,由直線與圓相切得![]() .然后將直線方程與橢圓方程聯立、消元,根據根與系數的關系由數量積可得
.然后將直線方程與橢圓方程聯立、消元,根據根與系數的關系由數量積可得![]() ,從而可得
,從而可得![]() .綜上可得
.綜上可得![]() 為定值.
為定值.
(1)由題意得![]()
![]() ,
,
∴橢圓![]() 的方程為
的方程為![]()
(2)①當直線![]() 的斜率不存在時,因為直線與圓相切,所以直線
的斜率不存在時,因為直線與圓相切,所以直線![]() 方程為
方程為![]() .
.
當![]() 時,可得M、N兩點坐標分別為
時,可得M、N兩點坐標分別為![]() ,
,
![]() ,
,![]() .
.
當![]() 時,同理可得
時,同理可得![]() ;
;
②當![]() 的斜率存在時,設
的斜率存在時,設![]() ,
,
由題意得![]() ,
,![]() ,
,
由![]() ,消去
,消去![]() 整理得
整理得![]() ,
,
∵直線![]() 與圓相交,∴
與圓相交,∴![]()
設![]() ,則
,則![]() ,
,![]() ,
,
![]() ,
,
![]() .
.
綜上![]() (定值) .
(定值) .


科目:高中數學 來源: 題型:
【題目】在直角坐標系![]() 中,已知橢圓
中,已知橢圓![]() ,若圓
,若圓![]()
![]() 的一條切線與橢圓
的一條切線與橢圓![]() 有兩個交點
有兩個交點![]() ,且
,且![]() .
.
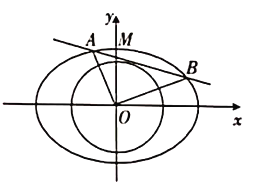
(1)求圓![]() 的方程;
的方程;
(2)已知橢圓![]() 的上頂點為
的上頂點為![]() ,點
,點![]() 在圓
在圓![]() 上,直線
上,直線![]() 與橢圓
與橢圓![]() 相交于另一點
相交于另一點![]() ,且
,且![]() ,求直線
,求直線![]() 的方程.
的方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,三棱柱![]() 的底面是正三角形,
的底面是正三角形,![]() 底面
底面![]() ,M為
,M為![]() 的中點.
的中點.
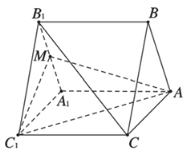
(1)求證:![]() 平面
平面![]() ;
;
(2)若![]() ,且沿側棱
,且沿側棱![]() 展開三棱柱的側面,得到的側面展開圖的對角線長為
展開三棱柱的側面,得到的側面展開圖的對角線長為![]() ,求作點
,求作點![]() 在平面
在平面![]() 內的射影H,請說明作法和理由,并求線段AH的長.
內的射影H,請說明作法和理由,并求線段AH的長.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】![]() 世紀中葉,中國數學家賈憲給出了直到六次冪的二項式系數表,如圖所示是《楊輝詳解九章算法》開方作法本原,其中第
世紀中葉,中國數學家賈憲給出了直到六次冪的二項式系數表,如圖所示是《楊輝詳解九章算法》開方作法本原,其中第![]() 層即為
層即為![]() 展開式的系數.賈憲稱整張數表為“開放作法本原”,今稱“賈憲三角”但賈憲未給出二項式系數的一般公式,因而未能建立一般正整數次冪的二項式定理.賈憲的數學著作已失傳,
展開式的系數.賈憲稱整張數表為“開放作法本原”,今稱“賈憲三角”但賈憲未給出二項式系數的一般公式,因而未能建立一般正整數次冪的二項式定理.賈憲的數學著作已失傳,![]() 世紀數學家楊輝在《詳解九章算法》
世紀數學家楊輝在《詳解九章算法》![]() 中引用了開放作法本原圖,注明此圖出“《釋鎖算數》,賈憲用此術”,因而流傳至今.只是后人往往因此把它誤稱為“楊輝三角”.
中引用了開放作法本原圖,注明此圖出“《釋鎖算數》,賈憲用此術”,因而流傳至今.只是后人往往因此把它誤稱為“楊輝三角”.![]() 展開式中
展開式中![]() 的系數為
的系數為![]() ,①則實數
,①則實數![]() 的值為_______________,②展開式中各項系數之和為__________________.
的值為_______________,②展開式中各項系數之和為__________________.

查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在直角坐標系![]() 中,曲線
中,曲線![]() 的參數方程為
的參數方程為![]() (
(![]() 為參數),若以
為參數),若以![]() 為極點,
為極點,![]() 軸正半軸為極軸建立極坐標系,曲線
軸正半軸為極軸建立極坐標系,曲線![]() 的極坐標方程為
的極坐標方程為![]() .
.
(1)求曲線![]() 的普通方程與曲線
的普通方程與曲線![]() 的直角坐標方程;
的直角坐標方程;
(2)若![]() 是曲線
是曲線![]() 上的任意一點,
上的任意一點,![]() 是曲線
是曲線![]() 上的任意一點,求線段
上的任意一點,求線段![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在直角坐標系![]() 中,以坐標原點為極點,
中,以坐標原點為極點,![]() 軸正半軸為極軸建立極坐標系,曲線
軸正半軸為極軸建立極坐標系,曲線![]() 的極坐標方程為
的極坐標方程為![]() .
.![]() 為曲線
為曲線![]() 上的動點,點
上的動點,點![]() 在射線
在射線![]() 上,且滿足
上,且滿足![]() .
.
(Ⅰ)求點![]() 的軌跡
的軌跡![]() 的直角坐標方程;
的直角坐標方程;
(Ⅱ)設![]() 與
與![]() 軸交于點
軸交于點![]() ,過點
,過點![]() 且傾斜角為
且傾斜角為![]() 的直線
的直線![]() 與
與![]() 相交于
相交于![]() 兩點,求
兩點,求![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知某中學高三文科班學生的數學與語文的水平測試成績抽樣統計如下表:
數學(x)
語文(y) | 90分~100分 (數A) | 80分~90分 (數B) | 60分~80分 (數C) |
90分~100分 (語A) | 20 | 7 | 5 |
80分~90分 (語B) | 18 | 9 | 6 |
60分~80分 (語C) | 4 | a | b |
設x,y分別表示數學成績與語文成績,若抽取學生n人,成績在90分~100分者記為A等級(優秀),成績在80分~90分者記為B等級(良好),成績在60分~80分者記為C等級(及格).例如:表中數學成績為A等級的共有![]() 人.已知x與y均為B等級的概率是0.09.
人.已知x與y均為B等級的概率是0.09.
(1)若在該樣本中,數學成績良好率是30%,求a,b的值;
(2)在語文成績為C等級的學生中,已知![]() ,
,![]() ,求數學成績為B等級的人數比C等級的人數少的概率.
,求數學成績為B等級的人數比C等級的人數少的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】現在給出三個條件:①a=2;②B![]() ;③c
;③c![]() b.試從中選出兩個條件,補充在下面的問題中,使其能夠確定△ABC,并以此為依據,求△ABC的面積.
b.試從中選出兩個條件,補充在下面的問題中,使其能夠確定△ABC,并以此為依據,求△ABC的面積.
在△ABC中,a、b、c分別是角A、B、C的對邊,且滿足![]() ,求△ABC的面積(選出一種可行的方案解答,若選出多個方案分別解答,則按第一個解答記分)
,求△ABC的面積(選出一種可行的方案解答,若選出多個方案分別解答,則按第一個解答記分)
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com