
【題目】對于定義城為R的函數![]() ,若滿足:①
,若滿足:①![]() ;②當
;②當![]() ,且
,且![]() 時,都有
時,都有![]() ;③當
;③當![]() 且
且![]() 時,都有
時,都有![]() ,則稱
,則稱![]() 為“偏對稱函數”.下列函數是“偏對稱函數”的是( )
為“偏對稱函數”.下列函數是“偏對稱函數”的是( )
A.![]() B.
B.![]()
C.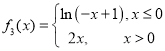 D.
D.![]()
【答案】BC
【解析】
運用新定義,分別討論四個函數是否滿足三個條件,結合奇偶性和單調性,以及對稱性,即可得到所求結論.
解:經驗證,![]() ,
,![]() ,
,![]() ,
,![]() 都滿足條件①;
都滿足條件①;
![]() ,或
,或![]() ;
;
當![]() 且
且![]() 時,等價于
時,等價于![]() ,
,
即條件②等價于函數![]() 在區間
在區間![]() 上單調遞減,在區間
上單調遞減,在區間![]() 上單調遞增;
上單調遞增;
A中,![]() ,
,![]() ,則當
,則當![]() 時,由
時,由![]() ,得
,得![]() ,不符合條件②,故
,不符合條件②,故![]() 不是“偏對稱函數”;
不是“偏對稱函數”;
B中,![]() ,
,![]() ,當
,當![]() 時,
時,![]() ,
,![]() ,當
,當![]() 時,
時,![]() ,
,![]() ,則當
,則當![]() 時,都有
時,都有![]() ,符合條件②,
,符合條件②,
∴函數![]() 在
在![]() 上單調遞減,在
上單調遞減,在![]() 上單調遞增,
上單調遞增,
由![]() 的單調性知,當
的單調性知,當![]() 時,
時,![]() ,
,
∴![]() ,
,
令![]() ,
,![]() ,
,![]() ,
,
當且僅當![]() 即
即![]() 時,“
時,“![]() ”成立,
”成立,
∴![]() 在
在![]() ,
,![]() 上是減函數,∴
上是減函數,∴![]() ,即
,即![]() ,符合條件③,
,符合條件③,
故![]() 是“偏對稱函數”;
是“偏對稱函數”;
C中,由函數 ,當
,當![]() 時,
時,![]() ,當
,當![]() 時,
時,![]() ,符合條件②,
,符合條件②,
∴函數![]() 在
在![]() 上單調遞減,在
上單調遞減,在![]() 上單調遞增,
上單調遞增,
有單調性知,當![]() 時,
時,![]() ,
,
設![]() ,
,![]() ,則
,則![]() ,
,
![]() 在
在![]() 上是減函數,可得
上是減函數,可得![]() ,
,
∴![]()
![]() ,
,
即![]() ,符合條件③,故
,符合條件③,故![]() 是“偏對稱函數”;
是“偏對稱函數”;
D中,![]() ,則
,則![]() ,則
,則![]() 是偶函數,
是偶函數,
而![]()
![]() (
(![]() ),則根據三角函數的性質可知,當
),則根據三角函數的性質可知,當![]() 時,
時,![]() 的符號有正有負,不符合條件②,故
的符號有正有負,不符合條件②,故![]() 不是“偏對稱函數”;
不是“偏對稱函數”;
故選:BC.


 學練快車道快樂假期暑假作業新疆人民出版社系列答案
學練快車道快樂假期暑假作業新疆人民出版社系列答案 浙大優學小學年級銜接導與練浙江大學出版社系列答案
浙大優學小學年級銜接導與練浙江大學出版社系列答案 小學暑假作業東南大學出版社系列答案
小學暑假作業東南大學出版社系列答案 津橋教育暑假拔高銜接廣東人民出版社系列答案
津橋教育暑假拔高銜接廣東人民出版社系列答案 波波熊暑假作業江西人民出版社系列答案
波波熊暑假作業江西人民出版社系列答案科目:高中數學 來源: 題型:
【題目】函數f(x)的定義域D={x|x≠0},且滿足對于任意x1,x2∈D.有f(x1·x2)=f(x1)+f(x2).
(1)求f(1)的值;
(2)判斷f(x)的奇偶性并證明;
(3)如果f(4)=1,f(3x+1)+f(2x-6)≤3,且f(x)在(0,+∞)上是增函數,求x的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖是2020年2月1日到2月20日,某地區新型冠狀病毒疫情新增數據的走勢圖.
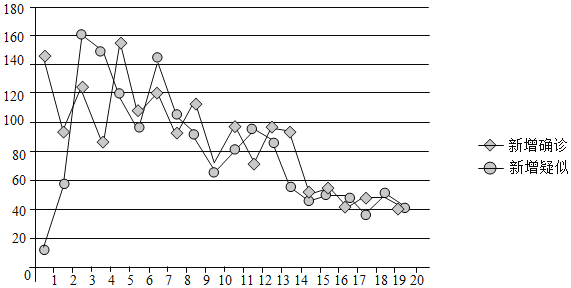
(Ⅰ)從這20天中任選1天,求新增確診和新增疑似的人數都超過100的概率;
(Ⅱ)從新增確診的人數超過100的日期中任選兩天,用X表示新增確診的人數超過140的天數,求X的分布列和數學期望;
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在直角坐標系中,過點![]() 的直線
的直線![]() 的參數方程為:
的參數方程為: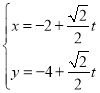 (
(![]() 為參數), 以原點為極點,
為參數), 以原點為極點,![]() 軸的正半軸為極軸建立極坐標系,已知曲線
軸的正半軸為極軸建立極坐標系,已知曲線![]()
![]() ,直線
,直線![]() 與曲線
與曲線![]() 分別交于
分別交于![]() 兩點.
兩點.
(1)寫出曲線![]() 和
和![]() 的普通方程;
的普通方程;
(2)若![]() 成等比數列,求
成等比數列,求![]() 值.
值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】2020年寒假是特殊的寒假,因為疫情全體學生只能在家進行網上在線學習,為了研究學生在網上學習的情況,某學校在網上隨機抽取120名學生對線上教育進行調查,其中男生與女生的人數之比為11∶13,其中男生30人對于線上教育滿意,女生中有15名表示對線上教育不滿意.
(1)完成![]() 列聯表,并回答能否有99%的把握認為對“線上教育是否滿意與性別有關”;
列聯表,并回答能否有99%的把握認為對“線上教育是否滿意與性別有關”;
滿意 | 不滿意 | 總計 | |
男生 | |||
女生 | |||
合計 | 120 |
(2)從被調查中對線上教育滿意的學生中,利用分層抽樣抽取8名學生,再在8名學生中抽取3名學生,作線上學習的經驗介紹,其中抽取男生的個數為![]() ,求出
,求出![]() 的分布列及期望值.
的分布列及期望值.
參考公式:附:![]()
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 0.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10828 |
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某造船公司年造船量是20艘,已知造船![]() 艘的產值函數為
艘的產值函數為![]() (單位:萬元),成本函數為
(單位:萬元),成本函數為![]() (單位:萬元),又在經濟學中,函數
(單位:萬元),又在經濟學中,函數![]() 的邊際函數
的邊際函數![]() 定義為
定義為![]() .
.
(1)求利潤函數![]() 及邊際利潤函數
及邊際利潤函數![]() .(提示:利潤=產值-成本)
.(提示:利潤=產值-成本)
(2)問年造船量安排多少艘時,可使公司造船的年利潤最大?
(3)求邊際利潤函數![]() 的單調遞減區間,并說明單調遞減在本題中的實際意義是什么?
的單調遞減區間,并說明單調遞減在本題中的實際意義是什么?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() ,函數g(x)=2﹣f(﹣x).
,函數g(x)=2﹣f(﹣x).
(1)判斷函數g(x)的奇偶性;
(2)若x∈(﹣1,0),
①求f(x)的值域;
②g(x)<tf(x)恒成立,求實數t的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在直角坐標系![]() 中,圓
中,圓![]() 的參數方程為
的參數方程為![]() (
(![]() 為參數),圓
為參數),圓![]() 與圓
與圓![]() 外切于原點
外切于原點![]() ,且兩圓圓心的距離
,且兩圓圓心的距離![]() ,以坐標原點為極點,
,以坐標原點為極點,![]() 軸正半軸為極軸建立極坐標系.
軸正半軸為極軸建立極坐標系.
(1)求圓![]() 和圓
和圓![]() 的極坐標方程;
的極坐標方程;
(2)過點![]() 的直線
的直線![]() ,
,![]() 與圓
與圓![]() 異于點
異于點![]() 的交點分別為點
的交點分別為點![]() ,
,![]() ,與圓
,與圓![]() 異于點
異于點![]() 的交點分別為點
的交點分別為點![]() ,
,![]() ,且
,且![]() ,求四邊形面積
,求四邊形面積![]() 的最大值.
的最大值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com