
【題目】已知P為△ABC內一點,且滿足 ![]() ,記△ABP,△BCP,△ACP的面積依次為S1 , S2 , S3 , 則S1:S2:S3等于( )
,記△ABP,△BCP,△ACP的面積依次為S1 , S2 , S3 , 則S1:S2:S3等于( )
A.1:2:3
B.1:4:9
C.2:3:1
D.3:1:2
【答案】D
【解析】解:如圖:設D、E 分別為BC、AC的中點,
∵ ![]() =0,∴
=0,∴ ![]() ﹣
﹣ ![]() =﹣3(
=﹣3( ![]() +
+ ![]() ),
),
∴ ![]() =﹣3×2
=﹣3×2 ![]() =﹣6
=﹣6 ![]() ,
,
同理由( ![]() +
+ ![]() )=﹣2(
)=﹣2( ![]() +
+ ![]() ),即 2
),即 2 ![]() =﹣2×
=﹣2× ![]() ,
,
∴ ![]() =﹣
=﹣ ![]()
![]() .∴P到BC的距離等于A到BC的距離的
.∴P到BC的距離等于A到BC的距離的 ![]() ,
,
設△ABC的面積為S,則S2 = ![]() S.
S.
P到AC的距離等于B到AC的距離的 ![]() ,
,
∴S3 = ![]() S.∴S1 =S﹣S2﹣S3 =
S.∴S1 =S﹣S2﹣S3 = ![]() S.
S.
∴S1:S2:S3= ![]() S:
S: ![]() S=
S= ![]() S=3:1:2,
S=3:1:2,
故選D.
根據已知的等式變形可得 ![]() =﹣6
=﹣6 ![]() ,
, ![]() =﹣
=﹣ ![]()
![]() ,從而得出P到BC的距離等于A到BC的距離的
,從而得出P到BC的距離等于A到BC的距離的 ![]() ,P到AC的距離等于B到AC的距離的
,P到AC的距離等于B到AC的距離的 ![]() .從而有S2 =
.從而有S2 = ![]() S,S3 =
S,S3 = ![]() S,S1 =S﹣S2﹣S3 =
S,S1 =S﹣S2﹣S3 = ![]() S即可解決問題.
S即可解決問題.


科目:高中數學 來源: 題型:
【題目】(文科)某出租車公司響應國家節能減排的號召,已陸續購買了140輛純電動汽車作為運營車輛,目前我國主流純電動汽車按續駛里程數![]() (單位:公里)分為3類,即
(單位:公里)分為3類,即![]() ,
, ![]() ,
, ![]() .對這140輛車的行駛總里程進行統計,結果如下表:
.對這140輛車的行駛總里程進行統計,結果如下表:

(1)從這140輛汽車中任取1輛,求該車行駛總里程超過5萬公里的概率; (2)公司為了了解這些車的工作狀況,決定抽取14輛車進行車況分析,按表中描述的六種情況進行分層抽樣,設從![]() 類車中抽取了
類車中抽取了![]() 輛車. (ⅰ)求
輛車. (ⅰ)求![]() 的值; (ⅱ)如果從這
的值; (ⅱ)如果從這![]() 輛車中隨機選取2輛車,求恰有1輛車行駛總里程超過5萬公里的概率.
輛車中隨機選取2輛車,求恰有1輛車行駛總里程超過5萬公里的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】(本小題共l2分)
如圖,在直三棱柱ABC-A1B1C1中,∠BAC=90°,AB=AC=AA1=1,延長A1C1至點P,使C1P=A1C1,連接AP交棱CC1于D.
(Ⅰ)求證:PB1∥平面BDA1;
(Ⅱ)求二面角A-A1D-B的平面角的余弦值;
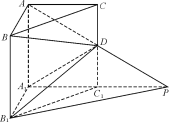
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某企業為了解下屬某部門對本企業職工的服務情況,隨機訪問50名職工,根據這50名職工對該部門的評分,繪制頻率分布直方圖(如圖所示),其中樣本數據分組區間為[40,50],[50,60],…,[80,90],[90,100] 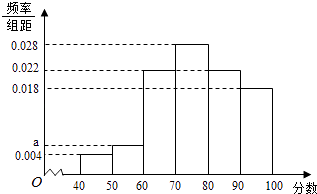
(1)求頻率分布圖中a的值;
(2)估計該企業的職工對該部門評分不低于80的概率;
(3)從評分在[40,60]的受訪職工中,隨機抽取2人,求此2人評分都在[40,50]的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在△ABC中,內角A,B,C對邊的邊長分別是a,b,c,已知c=2,C= ![]() .
.
(1)若△ABC的面積等于 ![]() ,求a,b;
,求a,b;
(2)若sinC+sin(B﹣A)=2sin2A,求△ABC的面積.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在一次![]() 公里的自行車個人賽中,25名參賽選手的成績(單位:分鐘)的莖葉圖如圖所示:
公里的自行車個人賽中,25名參賽選手的成績(單位:分鐘)的莖葉圖如圖所示:

(1)現將參賽選手按成績由好到差編為1~25號,再用系統抽樣方法從中選取5人,已知選手甲的成績為85分鐘,若甲被選取,求被選取的其余4名選手的成績的平均數;
(2)若從總體中選取一個樣本,使得該樣本的平均水平與總體相同,且樣本的方差不大于7,則稱選取的樣本具有集中代表性,試從總體(25名參賽選手的成績)選取一個具有集中代表性且樣本容量為5的樣本,并求該樣本的方差.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知△ABC的三個內角A、B、C的對邊分別為a、b、c,且b2+c2=a2+bc,求:
(1)2sinBcosC﹣sin(B﹣C)的值;
(2)若a=2,求△ABC周長的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設定義在區間![]() 上的函數
上的函數![]() 的圖象為
的圖象為![]() ,
, ![]() 、
、![]() ,且
,且![]() 為圖象
為圖象![]() 上的任意一點,
上的任意一點, ![]() 為坐標原點,當實數
為坐標原點,當實數![]() 滿足
滿足![]() 時,記向量
時,記向量![]() ,若
,若![]() 恒成立,則稱函數
恒成立,則稱函數![]() 在區間
在區間![]() 上可在標準
上可在標準![]() 下線性近似,其中
下線性近似,其中![]() 是一個確定的正數.
是一個確定的正數.
(1)設函數![]() 在區間
在區間![]() 上可在標準
上可在標準![]() 下線性近似,求
下線性近似,求![]() 的取值范圍;
的取值范圍;
(2)已知函數![]() 的反函數為
的反函數為![]() ,函數
,函數![]() ,(
,( ![]() ),點
),點![]() 、
、![]() ,記直線
,記直線![]() 的斜率為
的斜率為![]() ,若
,若![]() ,問:是否存在
,問:是否存在![]() ,使
,使![]() 成立?若存在,求
成立?若存在,求![]() 的取值范圍;若不存在,請說明理由.
的取值范圍;若不存在,請說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com