
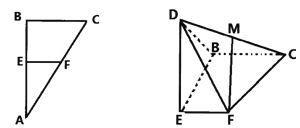
【題目】如圖在直角![]() 中,
中,![]() 為直角,
為直角,![]() ,
,![]() ,
,![]() 分別為
分別為![]() ,
,![]() 的中點,將
的中點,將![]() 沿
沿![]() 折起,使點
折起,使點![]() 到達點
到達點![]() 的位置,連接
的位置,連接![]() ,
,![]() ,
,![]() 為
為![]() 的中點.
的中點.
(Ⅰ)證明:![]() 面
面![]() ;
;
(Ⅱ)若![]() ,求二面角
,求二面角![]() 的余弦值.
的余弦值.
科目:高中數學 來源: 題型:
【題目】[選修4-4:坐標系與參數方程]
在直角坐標系![]() 中,曲線
中,曲線![]() :
:![]() (
(![]() ,
,![]() 為參數).在以坐標原點為極點,
為參數).在以坐標原點為極點,![]() 軸的正半軸為極軸的極坐標系中,曲線
軸的正半軸為極軸的極坐標系中,曲線![]() :
:![]() .
.
(1)說明![]() 是哪一種曲線,并將
是哪一種曲線,并將![]() 的方程化為極坐標方程;
的方程化為極坐標方程;
(2)若直線![]() 的方程為
的方程為![]() ,設
,設![]() 與
與![]() 的交點為
的交點為![]() ,
,![]() ,
,![]() 與
與![]() 的交點為
的交點為![]() ,
,![]() ,若
,若![]() 的面積為
的面積為![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知點![]() 和橢圓
和橢圓![]() . 直線
. 直線![]() 與橢圓
與橢圓![]() 交于不同的兩點
交于不同的兩點![]() .
.
(Ⅰ) 求橢圓![]() 的離心率;
的離心率;
(Ⅱ) 當![]() 時,求
時,求![]() 的面積;
的面積;
(Ⅲ)設直線![]() 與橢圓
與橢圓![]() 的另一個交點為
的另一個交點為![]() ,當
,當![]() 為
為![]() 中點時,求
中點時,求![]() 的值 .
的值 .
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() ,曲線
,曲線![]() 在點
在點![]() 的切線方程為
的切線方程為![]() .
.
(1)求實數![]() 的值,并求
的值,并求![]() 的極值.
的極值.
(2)是否存在![]() ,使得
,使得![]() 對任意
對任意![]() 恒成立?若存在,求出
恒成立?若存在,求出![]() 的最小值;若不存在,請說明理由.
的最小值;若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】以下關于圓錐曲線的命題中:①雙曲線![]() 與橢圓
與橢圓![]() 有相同的焦點;②設
有相同的焦點;②設![]() 、
、![]() 是兩個定點,
是兩個定點,![]() 為非零常數,若
為非零常數,若![]() ,則動點
,則動點![]() 的軌跡為雙曲線的一支;③設點
的軌跡為雙曲線的一支;③設點![]() 、
、![]() 分別是定圓
分別是定圓![]() 上一個定點和動點,
上一個定點和動點,![]() 為坐標原點,若
為坐標原點,若![]() ,則動點
,則動點![]() 的軌跡為圓;其中真命題是_________.(寫出所有真命題的序號)
的軌跡為圓;其中真命題是_________.(寫出所有真命題的序號)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知數列![]() 的前
的前![]() 項和為
項和為![]() .數列
.數列![]() 滿足
滿足![]() ,
,![]() .
.
(1)若![]() ,且
,且![]() ,求正整數
,求正整數![]() 的值;
的值;
(2)若數列![]() ,
,![]() 均是等差數列,求
均是等差數列,求![]() 的取值范圍;
的取值范圍;
(3)若數列![]() 是等比數列,公比為
是等比數列,公比為![]() ,且
,且![]() ,是否存在正整數
,是否存在正整數![]() ,使
,使![]() ,
,![]() ,
,![]() 成等差數列,若存在,求出一個
成等差數列,若存在,求出一個![]() 的值,若不存在,請說明理由.
的值,若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
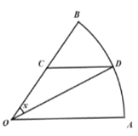
【題目】為慶祝某校一百周年校慶,展示該校一百年來的辦學成果及優秀校友風采,學校準備校慶期間搭建一個扇形展覽區,如圖,是一個半徑為2百米,圓心角為![]() 的扇形展示區的平面示意圖.點
的扇形展示區的平面示意圖.點![]() 是半徑
是半徑![]() 上一點,點
上一點,點![]() 是圓弧
是圓弧![]() 上一點,且
上一點,且![]() .為了實現“以展養展”,現決定:在線段
.為了實現“以展養展”,現決定:在線段![]() 、線段
、線段![]() 及圓弧
及圓弧![]() 三段所示位置設立廣告位,經測算廣告位出租收入是:線段
三段所示位置設立廣告位,經測算廣告位出租收入是:線段![]() 處每百米為
處每百米為![]() 元,線段
元,線段![]() 及圓弧
及圓弧![]() 處每百米均為
處每百米均為![]() 元.設
元.設![]() 弧度,廣告位出租的總收入為
弧度,廣告位出租的總收入為![]() 元.
元.
(1)求![]() 關于
關于![]() 的函數解析式,并指出該函數的定義域;
的函數解析式,并指出該函數的定義域;
(2)試問![]() 為何值時,廣告位出租的總收入最大,并求出其最大值.
為何值時,廣告位出租的總收入最大,并求出其最大值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com