考點:兩角和與差的正弦函數,二倍角的余弦,正弦函數的定義域和值域
專題:常規題型,三角函數的圖像與性質
分析:(1)利用和差公式及倍角公式化成正弦型函數的標準形式,然后根據正弦函數的單調區間求f(x)的單調區間,進而證明區間[-
,
]是f(x)的單調區間的一個子區間;
(2)根據x的取值范圍求出2x+
的范圍,然后求出2sin(2x+
)的范圍,即可得到f(x)的最大值與最小值.
解答:
解:(1)函數f(x)=2cosxsin(x+
)-
sin
2x+sinxcosx
=2cosx(
sinx+
cosx)-
(1-cos2x)+
sin2x
=sinxcosx+
cos
2x-
+cos2x+
sin2x=sin2x+
cos2x
=2sin(2x+
),
由
-+2kπ≤2x+≤+2kπ得:
-+kπ≤x≤+kπ,(k∈Z)
當k=0時,函數f(x)的一個單調遞增區間為[
-,
],
又∵[
-,]⊆[
-,
],
∴f(x)在[-
,
]上遞增;
(2)∵x∈[0,
],∴2x+
∈[
,]
∴
-≤2sin(2x+
)≤2
∴求f(x)的最大值為2,最小值為
-.
點評:本題考查了三角變換及三角函數的性質,解決本題的關鍵是把函數表達式化成正弦型函數的標準形式,根據正弦函數的性質研究函數f(x)的性質.



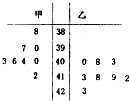 為調查甲乙兩人網站受歡迎的程度,隨機選取了某個月1號至8號,統計這8天內每天同一時間段的點擊量,得到如圖所示的莖葉圖.
為調查甲乙兩人網站受歡迎的程度,隨機選取了某個月1號至8號,統計這8天內每天同一時間段的點擊量,得到如圖所示的莖葉圖.