
【題目】設![]()
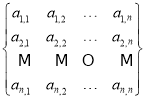 是由
是由![]() 組成的
組成的![]() 行
行![]() 列的數表(每個數恰好出現一次),
列的數表(每個數恰好出現一次),![]() 且
且![]() .
.
若存在![]() ,
, ![]() ,使得
,使得![]() 既是第
既是第![]() 行中的最大值,也是第
行中的最大值,也是第![]() 列中的最小值,則稱數表
列中的最小值,則稱數表![]() 為一個“
為一個“![]() 數表”
數表”![]() 為數表
為數表![]() 的一個“
的一個“![]() 值”,
值”,
對任意給定的![]() ,所有“
,所有“![]() 數表”構成的集合記作
數表”構成的集合記作![]() .
.
判斷下列數表是否是“![]() 數表”.若是,寫出它的一個“
數表”.若是,寫出它的一個“![]() 值”;
值”;
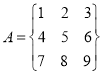 ,
, 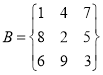
(Ⅱ)求證:若數表![]() 是“
是“![]() 數表”,則
數表”,則![]() 的“
的“![]() 值”是唯一的;
值”是唯一的;
(Ⅲ)在![]() 中隨機選取一個數表
中隨機選取一個數表![]() ,記
,記![]() 的“
的“![]() 值”為
值”為![]() ,求
,求![]() 的數學期望
的數學期望![]() .
.
【答案】(Ⅰ)見解析;(Ⅱ)見解析;(Ⅲ)見解析.
【解析】試題分析:
試題解析:(Ⅰ根據定義可得)![]() 是“
是“![]() 數表 ”,其“
數表 ”,其“![]() 值”為3,
值”為3, ![]() 不是“
不是“![]() 數表”.
數表”.
(Ⅱ)假設![]() 和
和![]() 均是數表
均是數表![]() 的“
的“![]() 值”,則分①若
值”,則分①若![]() , ②若
, ②若![]() ,③若
,③若![]() ,
, ![]() ,三種情況討論,得出矛盾. 即若數表
,三種情況討論,得出矛盾. 即若數表![]() 是“
是“![]() 數表”,則其“
數表”,則其“![]() 值”是唯一的.
值”是唯一的.
(Ⅲ)方法1:對任意的由![]() ,
, ![]() ,
, ![]() ,…,
,…, ![]() 組成的
組成的![]() 行
行![]() 列的數表
列的數表![]() .
.
定義數表![]() 如下,將數表
如下,將數表![]() 的第
的第![]() 行,第
行,第![]() 列的元素寫在數表
列的元素寫在數表![]() 的第
的第![]() 行,第
行,第![]() 列,即
列,即![]() (其中
(其中![]() ,
, ![]() ),討論其性質;定義數表
),討論其性質;定義數表![]() 如下,其與數表
如下,其與數表![]() 對應位置的元素的和為362,即
對應位置的元素的和為362,即![]() (其中
(其中![]() ,
, ![]() )
)
討論其性質,記![]() ,則
,則![]() ,即數表
,即數表![]() 與數表
與數表![]() 的“
的“![]() 值”之和為
值”之和為![]() ,
,
![]() 的數學期望
的數學期望![]() .
.
方法2:
![]() 所有可能的取值為
所有可能的取值為![]() .
.
記![]() 中使得
中使得![]() 的數表
的數表![]() 的個數記作
的個數記作![]() ,
, ![]() ,則
,則
![]() .
.
則![]() ,由此可求出
,由此可求出![]() 的數學期望
的數學期望![]() .
.
(Ⅰ)![]() 是“
是“![]() 數表 ”,其“
數表 ”,其“![]() 值”為3,
值”為3, ![]() 不是“
不是“![]() 數表”.
數表”.
(Ⅱ)假設![]() 和
和![]() 均是數表
均是數表![]() 的“
的“![]() 值”,
值”,
①若![]() ,則
,則![]() ;
;
②若![]() ,則
,則![]() ;
;
③若![]() ,
, ![]() ,則一方面
,則一方面
![]() ,
,
另一方面
![]() ;
;
矛盾. 即若數表![]() 是“
是“![]() 數表”,則其“
數表”,則其“![]() 值”是唯一的.
值”是唯一的.
(Ⅲ)方法1:
對任意的由![]() ,
, ![]() ,
, ![]() ,…,
,…, ![]() 組成的
組成的![]() 行
行![]() 列的數表
列的數表![]() .
.
定義數表![]() 如下,將數表
如下,將數表![]() 的第
的第![]() 行,第
行,第![]() 列的元素寫在數表
列的元素寫在數表![]() 的第
的第![]() 行,第
行,第![]() 列,即
列,即
![]() (其中
(其中![]() ,
, ![]() )
)
顯然有:
①數表![]() 是由
是由![]() ,
, ![]() ,
, ![]() ,…,
,…, ![]() 組成的
組成的![]() 行
行![]() 列的數表
列的數表
②數表![]() 的第
的第![]() 行的元素,即為數表
行的元素,即為數表![]() 的第
的第![]() 列的元素
列的元素
③數表![]() 的第
的第![]() 列的元素,即為數表
列的元素,即為數表![]() 的第
的第![]() 行的元素
行的元素
④若數表![]() 中,
中, ![]() 是第
是第![]() 行中的最大值,也是第
行中的最大值,也是第![]() 列中的最小值
列中的最小值
則數表![]() 中,
中, ![]() 是第
是第![]() 列中的最大值,也是第
列中的最大值,也是第![]() 行中的最小值.
行中的最小值.
定義數表![]() 如下,其與數表
如下,其與數表![]() 對應位置的元素的和為362,即
對應位置的元素的和為362,即
![]() (其中
(其中![]() ,
, ![]() )
)
顯然有
①數表![]() 是由
是由![]() ,
, ![]() ,
, ![]() ,…,
,…, ![]() 組成的
組成的![]() 行
行![]() 列的數表
列的數表
②若數表![]() 中,
中, ![]() 是第
是第![]() 列中的最大值,也是第
列中的最大值,也是第![]() 列中的最小值
列中的最小值
則數表![]() 中,
中, ![]() 是第
是第![]() 列中的最小值,也是第
列中的最小值,也是第![]() 列中的最大值
列中的最大值
特別地,對由![]() ,
, ![]() ,
, ![]() ,…,
,…, ![]() 組成的
組成的![]() 行
行![]() 列的數表
列的數表![]()
①數表![]() 是由
是由![]() ,
, ![]() ,
, ![]() ,…,
,…, ![]() 組成的
組成的![]() 行
行![]() 列的數表
列的數表
②若數表![]() 中,
中, ![]() 是第
是第![]() 行中的最大值,也是第
行中的最大值,也是第![]() 列中的最小值
列中的最小值
則數表![]() 中,
中, ![]() 是第
是第![]() 列中的最小值,也是第
列中的最小值,也是第![]() 列中的最大值
列中的最大值
即對任意的![]() ,其“
,其“![]() 值”為
值”為![]() (其中
(其中![]() ,
, ![]() ),則
),則![]() ,且其“
,且其“![]() 值”為
值”為![]() .
.
記![]() ,則
,則![]() ,即數表
,即數表![]() 與數表
與數表![]() 的“
的“![]() 值”之和為
值”之和為![]() ,
,
故可按照上述方式對![]() 中的數表兩兩配對,使得每對數表的 “
中的數表兩兩配對,使得每對數表的 “![]() 值”之和為
值”之和為![]() ,
,
故![]() 的數學期望
的數學期望![]() .
.
方法2:
![]() 所有可能的取值為
所有可能的取值為![]() .
.
記![]() 中使得
中使得![]() 的數表
的數表![]() 的個數記作
的個數記作![]() ,
, ![]() ,則
,則
![]() .
.
則![]() ,則
,則
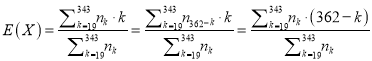 ,
,
故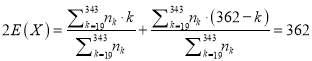 ,
, ![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:高中數學 來源: 題型:
【題目】已知曲線![]() :
:![]() (
(![]() 為參數)和曲線
為參數)和曲線![]() :
:![]() (
(![]() 為參數).
為參數).
(1)化![]() ,
,![]() 的方程為普通方程,并說明它們分別表示什么曲線;
的方程為普通方程,并說明它們分別表示什么曲線;
(2)若![]() 上的點
上的點![]() 對應的參數為
對應的參數為![]() ,
,![]() 為
為![]() 上的動點,求
上的動點,求![]() 中點
中點![]() 到直線
到直線![]() :
:![]() (
(![]() 為參數)距離的最小值及此時
為參數)距離的最小值及此時![]() 點的坐標.
點的坐標.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖所示,在正三棱柱ABC-A1B1C1中,已知D,E分別為BC,B1C1的中點,點F在棱CC1上,且EF⊥C1D.求證:
(1)直線A1E∥平面ADC1;
(2)直線EF⊥平面ADC1.

查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某幼兒園雛鷹班的生活老師統計2018年上半年每個月的20日的晝夜溫差![]() ,
,![]() 和患感冒的小朋友人數(
和患感冒的小朋友人數(![]() /人)的數據如下:
/人)的數據如下:
溫差 |
|
|
|
|
|
|
患感冒人數 | 8 | 11 | 14 | 20 | 23 | 26 |
其中![]() ,
,![]() ,
,![]() .
.
(Ⅰ)請用相關系數加以說明是否可用線性回歸模型擬合![]() 與
與![]() 的關系;
的關系;
(Ⅱ)建立![]() 關于
關于![]() 的回歸方程(精確到
的回歸方程(精確到![]() ),預測當晝夜溫差升高
),預測當晝夜溫差升高![]() 時患感冒的小朋友的人數會有什么變化?(人數精確到整數)
時患感冒的小朋友的人數會有什么變化?(人數精確到整數)
參考數據:![]() .參考公式:相關系數:
.參考公式:相關系數: ,回歸直線方程是
,回歸直線方程是![]() ,
, ,
,
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】(1)已知函數![]() ,其中
,其中![]() ,求函數
,求函數![]() 的圖象恰好經過第一、二、三象限的概率;
的圖象恰好經過第一、二、三象限的概率;
(2)某校早上8:10開始上課,假設該校學生小張與小王在早上7:30~8:00之間到校,且每人到該時間段內到校時刻是等可能的,求兩人到校時刻相差10分鐘以上的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】樹立和踐行“綠水青山就是金山銀山,堅持人與自然和諧共生”的理念越來越深入人心,已形成了全民自覺參與,造福百姓的良性循環.據此,某網站推出了關于生態文明建設進展情況的調查,大量的統計數據表明,參與調查者中關注此問題的約占80%.現從參與調查的人群中隨機選出![]() 人,并將這
人,并將這![]() 人按年齡分組:第1組
人按年齡分組:第1組![]() ,第2組
,第2組![]() ,第3組
,第3組![]() ,第4 組
,第4 組![]() ,第5組
,第5組![]() ,得到的頻率分布直方圖如圖所示
,得到的頻率分布直方圖如圖所示
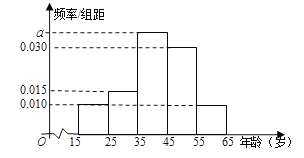
(1) 求![]() 的值
的值
(2)現在要從年齡較小的第1,2,3組中用分層抽樣的方法抽取![]() 人,再從這
人,再從這![]() 人中隨機抽取
人中隨機抽取![]() 人進行問卷調查,求在第1組已被抽到
人進行問卷調查,求在第1組已被抽到![]() 人的前提下,第3組被抽到
人的前提下,第3組被抽到![]() 人的概率;
人的概率;
(3)若從所有參與調查的人中任意選出![]() 人,記關注“生態文明”的人數為
人,記關注“生態文明”的人數為![]() ,求
,求![]() 的分布列與期望.
的分布列與期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系中,已知圓![]() 的方程為
的方程為![]() ,圓
,圓![]() 的方程為
的方程為![]() ,動圓
,動圓![]() 與圓
與圓![]() 內切且與圓
內切且與圓![]() 外切.
外切.
(1)求動圓圓心![]() 的軌跡
的軌跡![]() 的方程;
的方程;
(2)已知![]() 與
與![]() 為平面內的兩個定點,過
為平面內的兩個定點,過![]() 點的直線
點的直線![]() 與軌跡
與軌跡![]() 交于
交于![]() ,
,![]() 兩點,求四邊形
兩點,求四邊形![]() 面積的最大值.
面積的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]()
![]() 為偶函數,且函數
為偶函數,且函數![]() 的圖象的兩相鄰對稱軸間的距離為
的圖象的兩相鄰對稱軸間的距離為![]() .
.
(1)求![]() 的值;
的值;
(2)將函數![]() 的圖象向右平移
的圖象向右平移![]() 個單位長度后,再將得到的圖象上各點的橫坐標伸長為原來的4倍,縱坐標不變,得到函數
個單位長度后,再將得到的圖象上各點的橫坐標伸長為原來的4倍,縱坐標不變,得到函數![]() 的圖象,求函數
的圖象,求函數![]() 的單調遞減區間.
的單調遞減區間.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com