
【題目】據中國日報網報道:2017年11月13日,TOP500發布的最新一期全球超級計算機500強榜單顯示,中國超算在前五名中占據兩席,其中超算全球第一“神威太湖之光”完全使用了國產品牌處理器。為了了解國產品牌處理器打開文件的速度,某調查公司對兩種國產品牌處理器進行了12次測試,結果如下(數值越小,速度越快,單位是MIPS)
測試1 | 測試2 | 測試3 | 測試4 | 測試5 | 測試6 | 測試7 | 測試8 | 測試9 | 測試10 | 測試11 | 測試12 | |
品牌A | 3 | 6 | 9 | 10 | 4 | 1 | 12 | 17 | 4 | 6 | 6 | 14 |
品牌B | 2 | 8 | 5 | 4 | 2 | 5 | 8 | 15 | 5 | 12 | 10 | 21 |
設![]() 分別表示第次測試中品牌A和品牌B的測試結果,記
分別表示第次測試中品牌A和品牌B的測試結果,記![]()
![]()
(Ⅰ)求數據![]() 的眾數;
的眾數;
(Ⅱ)從滿足![]() 的測試中隨機抽取兩次,求品牌A的測試結果恰好有一次大于品牌B的測試結果的概率;
的測試中隨機抽取兩次,求品牌A的測試結果恰好有一次大于品牌B的測試結果的概率;
(Ⅲ)經過了解,前6次測試是打開含有文字和表格的文件,后6次測試是打開含有文字和圖片的文件.請你依據表中數據,運用所學的統計知識,對這兩種國產品牌處理器打開文件的速度進行評價.
【答案】(Ⅰ)4 ;(Ⅱ) ![]() ;(Ⅲ)本題為開放問題,答案不唯一.
;(Ⅲ)本題為開放問題,答案不唯一.
【解析】試題分析:(1)將自變量的取值情況寫出來,根據眾數的概念可得結果;(2)將題目中滿足從滿足![]() 的測試中隨機抽取兩次的事件次數數出來,滿足品牌A的測試結果恰好有一次大于品牌B的測試結果的次數數出來,兩個數據作比即可;(3)可以從題目中的條件中,從多個角度下結論,只要解釋的有道理均可得分。
的測試中隨機抽取兩次的事件次數數出來,滿足品牌A的測試結果恰好有一次大于品牌B的測試結果的次數數出來,兩個數據作比即可;(3)可以從題目中的條件中,從多個角度下結論,只要解釋的有道理均可得分。
解析:
(Ⅰ)
|
|
|
|
|
|
|
|
|
|
|
|
1 | 2 | 4 | 6 | 2 | 4 | 4 | 2 | 1 | 6 | 4 | 7 |
所以![]() 等于1有2次,
等于1有2次, ![]() =2有3次,
=2有3次, ![]() =4有4次,
=4有4次, ![]() =6有2次,
=6有2次, ![]() =7有1次,
=7有1次,
則數據![]() 的眾數為4
的眾數為4
(Ⅱ)設事件D=“品牌![]() 的測試結果恰有一次大于品牌
的測試結果恰有一次大于品牌![]() 的測試結果”.
的測試結果”.
滿足![]() 的測試共有4次,其中品牌
的測試共有4次,其中品牌![]() 的測試結果大于品牌
的測試結果大于品牌![]() 的測試結果有2次即測試3和測試7,不妨用M,N表示.品牌
的測試結果有2次即測試3和測試7,不妨用M,N表示.品牌![]() 的測試結果小于品牌
的測試結果小于品牌![]() 的測試結果有2次即測試6和測試11,不妨用P,Q表示.從中隨機抽取兩次,共有MN,MP,MQ,NP,NQ,PQ六種情況,其中事件D發生,指的是MP,MQ,NP,NQ四種情況.
的測試結果有2次即測試6和測試11,不妨用P,Q表示.從中隨機抽取兩次,共有MN,MP,MQ,NP,NQ,PQ六種情況,其中事件D發生,指的是MP,MQ,NP,NQ四種情況.
故![]() .
.
(Ⅲ)本題為開放問題,答案不唯一,在此給出評價標準,并給出可能出現的答案情況,閱卷時按照標準酌情給分.
給出明確結論,1分,結合已有數據,能夠運用以下兩個標準中的任何一個陳述得出該結論的理由,2分.
可能出現的作答情況舉例,及對應評分標準如下:
結論一:,品牌![]() 處理器對含有文字與表格的文件的打開速度快一些,品牌
處理器對含有文字與表格的文件的打開速度快一些,品牌![]() 處理器對含有文字與圖片的文件的打開速度快一些。
處理器對含有文字與圖片的文件的打開速度快一些。
理由如下:從前6次測試(打開含有文字與表格的文件)來看,對于含有文字與表格的相同文件,品牌![]() 的測試有兩次打開速度比品牌
的測試有兩次打開速度比品牌![]() 快(數值小),品牌
快(數值小),品牌![]() 有四次比品牌
有四次比品牌![]() 快,從后6次測試(打開含有文字與圖片的文件)來看,對于含有文字與圖片的相同文件,品牌
快,從后6次測試(打開含有文字與圖片的文件)來看,對于含有文字與圖片的相同文件,品牌![]() 有四次打開速度比品牌
有四次打開速度比品牌![]() 快(數值小).
快(數值小).
結論二:從測試結果看,這兩種國產品牌處理器的文件的打開速度結論:品牌![]() 打開文件速度快一些
打開文件速度快一些
理由如下:品牌![]() 處理器對文件打開的測試結果的平均數估計為
處理器對文件打開的測試結果的平均數估計為![]() ,品牌
,品牌![]() 處理器對文件打開的測試結果的平均數估計為
處理器對文件打開的測試結果的平均數估計為![]() ,所以品牌
,所以品牌![]() 打開文件速度快一些.(且品牌
打開文件速度快一些.(且品牌![]() 方差較小)
方差較小)


科目:高中數學 來源: 題型:
【題目】已知曲線![]() 的參數方程為
的參數方程為![]() ,其中
,其中![]() 為參數,且
為參數,且![]() 在直角坐標系
在直角坐標系![]() 中,以坐標原點
中,以坐標原點![]() 為極點,以
為極點,以![]() 軸正半軸為極軸建立極坐標系.
軸正半軸為極軸建立極坐標系.
(1)求曲線![]() 的極坐標方程;
的極坐標方程;
(2)設![]() 是曲線
是曲線![]() 上的一點,直線
上的一點,直線![]() 被曲線
被曲線![]() 截得的弦長為
截得的弦長為![]() ,求
,求![]() 點的極坐標.
點的極坐標.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知![]() 為坐標原點,拋物線
為坐標原點,拋物線![]() 上在第一象限內的點
上在第一象限內的點![]() 到焦點的距離為
到焦點的距離為![]() ,曲線
,曲線![]() 在點
在點![]() 處的切線交
處的切線交![]() 軸于點
軸于點![]() ,直線
,直線![]() 經過點
經過點![]() 且垂直于
且垂直于![]() 軸.
軸.
(Ⅰ)求![]() 點的坐標;
點的坐標;
(Ⅱ)設不經過點![]() 和
和![]() 的動直線
的動直線![]() 交曲線
交曲線![]() 于點
于點![]() 和
和![]() ,交
,交![]() 于點
于點![]() ,若直線
,若直線![]() ,
,![]() ,
,![]() 的斜率依次成等差數列,試問:
的斜率依次成等差數列,試問:![]() 是否過定點?請說明理由.
是否過定點?請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知點![]() 在橢圓
在橢圓![]() 上,且橢圓的離心率為
上,且橢圓的離心率為![]() .
.
(1)求橢圓![]() 的方程;
的方程;
(2)若![]() 為橢圓
為橢圓![]() 的右頂點,點
的右頂點,點![]() 是橢圓
是橢圓![]() 上不同的兩點(均異于
上不同的兩點(均異于![]() )且滿足直線
)且滿足直線![]() 與
與![]() 斜率之積為
斜率之積為![]() .試判斷直線
.試判斷直線![]() 是否過定點,若是,求出定點坐標,若不是,說明理由.
是否過定點,若是,求出定點坐標,若不是,說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知點![]() 為拋物線
為拋物線![]() 的焦點,點
的焦點,點![]() 為點
為點![]() 關于原點的對稱點,點
關于原點的對稱點,點![]() 在拋物線
在拋物線![]() 上,則下列說法錯誤的是( )
上,則下列說法錯誤的是( )
A. 使得![]() 為等腰三角形的點
為等腰三角形的點![]() 有且僅有4個
有且僅有4個
B. 使得![]() 為直角三角形的點
為直角三角形的點![]() 有且僅有4個
有且僅有4個
C. 使得![]() 的點
的點![]() 有且僅有4個
有且僅有4個
D. 使得![]() 的點
的點![]() 有且僅有4個
有且僅有4個
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知點![]() 為拋物線
為拋物線![]() 的焦點,點
的焦點,點![]() 為點
為點![]() 關于原點的對稱點,點
關于原點的對稱點,點![]() 在拋物線
在拋物線![]() 上,則下列說法錯誤的是( )
上,則下列說法錯誤的是( )
A. 使得![]() 為等腰三角形的點
為等腰三角形的點![]() 有且僅有4個
有且僅有4個
B. 使得![]() 為直角三角形的點
為直角三角形的點![]() 有且僅有4個
有且僅有4個
C. 使得![]() 的點
的點![]() 有且僅有4個
有且僅有4個
D. 使得![]() 的點
的點![]() 有且僅有4個
有且僅有4個
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】(2018屆高三·湖南十校聯考)已知函數f(x)=x+sin x(x∈R),且f(y2-2y+3)+f(x2-4x+1)≤0,則當y≥1時, ![]() 的取值范圍是( )
的取值范圍是( )
A. ![]() B.
B. ![]()
C. [1,3![]() -3] D.
-3] D. ![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】選修4-4:坐標系與參數方程
在平面直角坐標系![]() 中,以坐標原點
中,以坐標原點![]() 為極點,以
為極點,以![]() 軸正半軸為極軸,建立極坐標系.曲線
軸正半軸為極軸,建立極坐標系.曲線![]() 的極坐標方程為
的極坐標方程為![]() ,曲線
,曲線![]() 的參數方程為
的參數方程為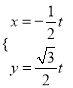 (
(![]() 為參數)
為參數)
(1)求曲線![]() 的直角坐標方程及曲線
的直角坐標方程及曲線![]() 的極坐標方程;
的極坐標方程;
(2)當![]() (
(![]() )時在曲線
)時在曲線![]() 上對應的點為
上對應的點為![]() ,若
,若![]() 的面積為
的面積為![]() ,求
,求![]() 點的極坐標,并判斷
點的極坐標,并判斷![]() 是否在曲線
是否在曲線![]() 上(其中點
上(其中點![]() 為半圓的圓心)
為半圓的圓心)
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com