
【題目】已知![]() ,
, ![]() 為實數,函數
為實數,函數![]() ,函數
,函數![]() .
.
(1) 當![]() 時,令
時,令![]() ,若
,若![]() 恒成立,求實數
恒成立,求實數![]() 的取值范圍;
的取值范圍;
(2) 當![]() 時,令
時,令![]() ,是否存在實數
,是否存在實數![]() ,使得對于函數
,使得對于函數![]() 定義域中的任意實數
定義域中的任意實數![]() ,均存在實數
,均存在實數![]() ,有
,有![]() 成立?若存在,求出實數
成立?若存在,求出實數![]() 的取值集合;若不存在,請說明理由.
的取值集合;若不存在,請說明理由.
【答案】(1)![]() ;(2)見解析
;(2)見解析
【解析】試題分析:(1)![]() 恒成立,等價于
恒成立,等價于![]() 恒成立,利用導數研究函數的單調性,求出
恒成立,利用導數研究函數的單調性,求出![]() 的最大值即可得結果;(2)
的最大值即可得結果;(2) ![]() 時,
時, ![]()
![]() ,對
,對![]() 分兩種情況討論,分別利用導數研究函數的單調性(需要兩次求導),利用單調性結合函數圖象,排除不合題意的
分兩種情況討論,分別利用導數研究函數的單調性(需要兩次求導),利用單調性結合函數圖象,排除不合題意的![]() 值進而可得
值進而可得
試題解析:(1) 當![]() 時,
時, ![]()
![]() 在
在![]() 上遞增,在
上遞增,在![]() 上遞減,可得
上遞減,可得![]() 的最大值為
的最大值為![]() ,所以可得)
,所以可得)![]() .
.
(2) 當a=-1時,假設存在實數b滿足條件,則G(x)=![]() lnx≥1在x∈(0,1)∪(1,+∞)上恒成立.
lnx≥1在x∈(0,1)∪(1,+∞)上恒成立.
1) 當x∈(0,1)時,G(x)=![]() lnx≥1可化為(bx+1-b)lnx-x+1≤0,
lnx≥1可化為(bx+1-b)lnx-x+1≤0,
令H(x)=(bx+1-b)lnx-x+1,x∈(0,1),
問題轉化為:H(x)≤0對任意x∈(0,1)恒成立(*);
則H(1)=0,H′(x)=blnx+![]() +b-1,H′(1)=0.
+b-1,H′(1)=0.
令Q(x)=blnx+![]() +b-1,則Q′(x)=
+b-1,則Q′(x)=![]() .
.
① b≤![]() 時,因為b(x+1)-1≤
時,因為b(x+1)-1≤![]() (x+1)-1<
(x+1)-1<![]() ×2-1=0,
×2-1=0,
故Q′(x)<0,所以函數y=Q(x)在x∈(0,1)時單調遞減,Q(x)>Q(1)=0,
即H′(x)>0,從而函數y=H(x)在x∈(0,1)時單調遞增,
故H(x)<H(1)=0,所以(*)成立,滿足題意;
② 當b>![]() ,Q′(x)=
,Q′(x)=![]() =
= ,
,
因為b>![]() ,所以
,所以![]() -1<1,記I=
-1<1,記I=![]() ∩(0,1),則當x∈I時,x-
∩(0,1),則當x∈I時,x-![]() >0,
>0,
故Q′(x)>0,所以函數y=Q(x)在x∈I時單調遞增,Q(x)<Q(1)=0,
即H′(x)<0,從而函數y=H(x)在x∈I時單調遞減,所以H(x)>H(1)=0,此時(*)不成立;
所以當x∈(0,1),G(x)=![]() lnx≥1恒成立時,b≤
lnx≥1恒成立時,b≤![]() ;
;
2) 當x∈(1,+∞)時,G(x)=![]() lnx≥1可化為(bx+1-b)lnx-x+1≥0,
lnx≥1可化為(bx+1-b)lnx-x+1≥0,
令H(x)=(bx+1-b)lnx-x+1,x∈(1,+∞),問題轉化為:
H(x)≥0對任意的x∈(1,+∞)恒成立(**);則H(1)=0,H′(x)=blnx+![]() +b-1,H′(1)=0.
+b-1,H′(1)=0.
令Q(x)=blnx+![]() +b-1,則Q′(x)=
+b-1,則Q′(x)=![]() .
.
① b≥![]() 時,b(x+1)-1>2b-1≥
時,b(x+1)-1>2b-1≥![]() ×2-1=0,
×2-1=0,
故 Q′(x)>0,所以函數y=Q(x)在x∈(1,+∞)時單調遞增,Q(x)>Q(1)=0,即H′(x)>0,
從而函數y=H(x)在x∈(1,+∞)時單調遞增,所以H(x)>H(1)=0,此時(**)成立;
② 當b<![]() 時,
時,
ⅰ) 若 b≤0,必有Q′(x)<0,故函數y=Q(x)在x∈(1,+∞)上單調遞減,
所以Q(x)<Q(1)=0,即H′(x)<0,
從而函數y=H(x)在x∈(1,+∞)時單調遞減,所以H(x)<H(1)=0,此時(**)不成立;
ⅱ) 若0<b<![]() ,則
,則![]() -1>1,所以x∈
-1>1,所以x∈![]() 時,Q′(x)=
時,Q′(x)=![]() =
= <0,
<0,
故函數y=Q(x)在x∈![]() 上單調遞減,Q(x)<Q(1)=0,即H′(x)<0,
上單調遞減,Q(x)<Q(1)=0,即H′(x)<0,
所以函數y=H(x)在x∈![]() 時單調遞減,所以H(x)<H(1)=0,此時(**)不成立;
時單調遞減,所以H(x)<H(1)=0,此時(**)不成立;
所以當x∈(1,+∞),G(x)=![]() lnx≥1恒成立時,b≥
lnx≥1恒成立時,b≥![]() .(15分)
.(15分)
綜上所述,當x∈(0,1)∪(1,+∞),G(x)=![]() lnx≥1恒成立時,b=
lnx≥1恒成立時,b=![]() ,從而實數b的取值集合為
,從而實數b的取值集合為![]() .
.


 名校課堂系列答案
名校課堂系列答案科目:高中數學 來源: 題型:
【題目】如圖,直三棱柱![]() 中,
中,![]() ,
,![]() ,
,![]() 是
是![]() 的中點,
的中點,![]() 是等腰三角形,
是等腰三角形,![]() 為
為![]() 的中點,
的中點,![]() 為
為![]() 上一點.
上一點.
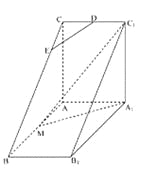
(I)若![]() 平面
平面![]() ,求
,求![]() ;
;
(II)平面![]() 將三棱柱
將三棱柱![]() 分成兩個部分,求較小部分與較大部分的體積之比.
分成兩個部分,求較小部分與較大部分的體積之比.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某校數學課外興趣小組為研究數學成績是否與性別有關,先統計本校高三年級每個學生一學期數學成績平均分(采用百分制),剔除平均分在![]() 分以下的學生后, 共有男生
分以下的學生后, 共有男生![]() 名,女生
名,女生![]() 名,現采用分層抽樣的方法,從中抽取了
名,現采用分層抽樣的方法,從中抽取了![]() 名學生,按性別分為兩組,并將兩組學生成績分為
名學生,按性別分為兩組,并將兩組學生成績分為![]() 組, 得到如下頻數分布表.
組, 得到如下頻數分布表.

(Ⅰ)估計男、女生各自的平均分(同一組數據用該組區間中點值作代表),從計算結果看,能否判斷數學成績與性別有關;
(Ⅱ)規定![]() 分以上為優分(含
分以上為優分(含![]() 分),請你根據已知條件完成
分),請你根據已知條件完成![]() 列聯表,并判斷是否有
列聯表,并判斷是否有![]() %以上的把握認為“數學成績與性別有關”,(
%以上的把握認為“數學成績與性別有關”,( 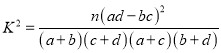 ,其中
,其中![]() )
)

查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】(本小題滿分12分)如圖,在三棱柱ABC-A1B1C1中,側棱垂直于底面,AB⊥BC,E、F分別為A1C1和BC的中點.
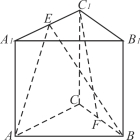
(1)求證:平面ABE⊥平面B1BCC1;
(2)求證:C1F//平面ABE.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】橢圓![]() :
: ![]() 的離心率為
的離心率為![]() ,過其右焦點
,過其右焦點![]() 與長軸垂直的直線與橢圓在第一象限相交于點
與長軸垂直的直線與橢圓在第一象限相交于點![]() ,
, ![]() .
.
(1)求橢圓![]() 的標準方程;
的標準方程;
(2)設橢圓![]() 的左頂點為
的左頂點為![]() ,右頂點為
,右頂點為![]() ,點
,點![]() 是橢圓上的動點,且點
是橢圓上的動點,且點![]() 與點
與點![]() ,
, ![]() 不重合,直線
不重合,直線![]() 與直線
與直線![]() 相交于點
相交于點![]() ,直線
,直線![]() 與直線
與直線![]() 相交于點
相交于點![]() ,求證:以線段
,求證:以線段![]() 為直徑的圓恒過定點.
為直徑的圓恒過定點.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設點![]() 、
、![]() 是平面上左、右兩個不同的定點,
是平面上左、右兩個不同的定點, ![]() ,動點
,動點![]() 滿足:
滿足:
![]() .
.
(1)求證:動點![]() 的軌跡
的軌跡![]() 為橢圓;
為橢圓;
(2)拋物線![]() 滿足:①頂點在橢圓
滿足:①頂點在橢圓![]() 的中心;②焦點與橢圓
的中心;②焦點與橢圓![]() 的右焦點重合.
的右焦點重合.
設拋物線![]() 與橢圓
與橢圓![]() 的一個交點為
的一個交點為![]() .問:是否存在正實數
.問:是否存在正實數![]() ,使得
,使得![]() 的邊長為連續自然數.若存在,求出
的邊長為連續自然數.若存在,求出![]() 的值;若不存在,說明理由.
的值;若不存在,說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某校夏令營有3名男同學A、B、C和3名女同學X,Y,Z,其年級情況如下表,現從這6名同學中隨機選出2人參加知識競賽(每人被選到的可能性相同).
(1)用表中字母列舉出所有可能的結果;
(2)設M為事件“選出的2人來自不同年級且恰有1名男同學和1名女同學”,求事件M發生的概率.
一年級 | 二年級 | 三年級 | |
男同學 | A | B | C |
女同學 | X | Y | Z |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com