Question

【題目】設點、是平面上左、右兩個不同的定點， ，動點滿足：

．

（1）求證：動點的軌跡為橢圓；

（2）拋物線滿足：①頂點在橢圓的中心；②焦點與橢圓的右焦點重合．

設拋物線與橢圓的一個交點為．問：是否存在正實數，使得的邊長為連續自然數．若存在，求出的值；若不存在，說明理由．

Answer 1

【答案】（1）見解析；（2）存在實數，使得的邊長為連續自然數。

【解析】試題分析: （1）根據題意，分兩種情況討論：①點P、F1、F2構成三角形，②點P、F1、F2不構成三角形，每種情況下分析可得|PF1|+|PF2|=4m，由橢圓的定義分析可得答案；

（2）根據題意，由（1）可得，動點P的軌跡方程，分析可得拋物線的焦點坐標，假設存在滿足條件的實數m，結合橢圓與拋物線的性質分析可得m的值，即可得答案．

試題解析

（1）若點構成三角形則

，

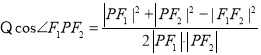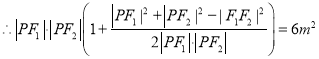
整理得，即．

若點不構成三角形，也滿足．

所以動點的軌跡為橢圓

（2）動點的軌跡方程為

拋物線的焦點坐標為與橢圓的右焦點重合．

假設存在實數，使得的邊長為連續自然數．

因為，

不妨設|，

由拋物線的定義可知，解得，

設點的坐標為，

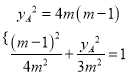
整理得，解得或

所以存在實數，使得的邊長為連續自然數