
已知函數 .
.
(1)求

 的解集;
的解集;
(2)設函數
 ,若
,若 對任意的
對任意的 都成立,求
都成立,求 的取值范圍.
的取值范圍.
(1)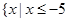 或
或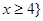 ;(2)
;(2)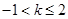 .
.
解析試題分析:本題主要考查絕對值不等式的解法、分段函數圖象、直線圖象等基礎知識,考查學生的轉化能力、計算能力和數形結合思想.第一問,先將被開方數寫成完全平方式,開方需要加絕對值,解絕對值不等式,利用零點分段法去掉絕對值符號,解不等式組;第二問,“ 對任意的
對任意的 都成立”轉化為“
都成立”轉化為“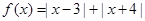 的圖象恒在
的圖象恒在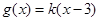 圖象的上方”利用零點分段法將絕對值去掉,轉化成分段函數,畫出分段函數圖象,而
圖象的上方”利用零點分段法將絕對值去掉,轉化成分段函數,畫出分段函數圖象,而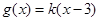 恒過(3,0)點,將
恒過(3,0)點,將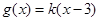 的直線繞(3,0)點旋轉,找出符合題意的位置,得到k的取值范圍.
的直線繞(3,0)點旋轉,找出符合題意的位置,得到k的取值范圍.
試題解析:(1)
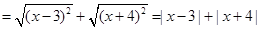
∴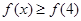 即
即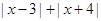
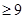
∴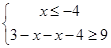 ①或
①或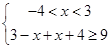 ②或
②或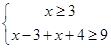 ③
③
解得不等式①: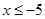 ;②:無解③:
;②:無解③: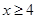
所以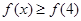 的解集為
的解集為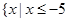 或
或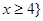 . 5分
. 5分
(2) 即
即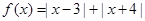 的圖象恒在
的圖象恒在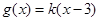 圖象的上方
圖象的上方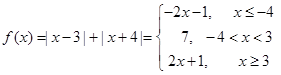
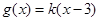 圖象為恒過定點
圖象為恒過定點
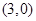 ,且斜率
,且斜率 變化的一條直線作函數
變化的一條直線作函數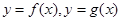 圖象如圖,其中
圖象如圖,其中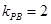 ,
, ,∴
,∴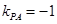
由圖可知,要使得 的圖象恒在
的圖象恒在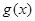 圖象的上方
圖象的上方
∴實數 的取值范圍為
的取值范圍為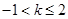 . 10分
. 10分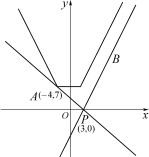
考點:絕對值不等式的解法、分段函數圖象、直線圖象.


科目:高中數學 來源: 題型:解答題
設函數f(x)= 其中b>0,c∈R.當且僅當x=-2時,函數f(x)取得最小值-2.
其中b>0,c∈R.當且僅當x=-2時,函數f(x)取得最小值-2.
(1)求函數f(x)的表達式;
(2)若方程f(x)=x+a(a∈R)至少有兩個不相同的實數根,求a取值的集合.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com