Question

【題目】某公司為確立下一年度投入某種產品的宣傳費，需了解年宣傳費（單位：千元）對年銷售量（單位： ）和年利潤（單位：千元）的影響.對近年的宣傳費和年銷售量數據作了初步處理，得到下面的散點圖及一些統計量的值.

表中

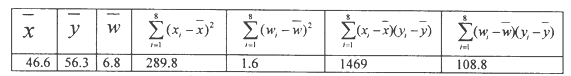
（Ⅰ）根據散點圖判斷， 與哪一個適宜作為年銷售量關于年宣傳費的回歸方程類型？（給出判斷即可，不必說明理由）

（Ⅱ）根據（Ⅰ）的判斷結果及表中數據，建立關于的回歸方程；

（Ⅲ）已知這種產品的年利率與的關系為.根據（Ⅱ）的結果回答下列問題：

（i）年宣傳費時，年銷售量及利潤的預報值是多少？

（ii）年宣傳費為何值時，年利率的預報值最大？

附：對于一組數據……，其回歸線的斜率和截距的最小二乘法估計分別為： ，

Answer 1

【答案】（1）適宜；（2）；（3）（i）；（ii）年宣傳費為46.24千元時，年利潤的預報值最大.

【解析】試題分析：（Ⅰ）根據散點圖，即可判斷出，
（Ⅱ）先建立中間量，，建立y關于w的線性回歸方程，根據公式求出w，問題得以解決；
（Ⅲ）（i）年宣傳費x=49時，代入到回歸方程，計算即可，
（ii）求出預報值得方程，根據函數的性質，即可求出．

試題解析：

（I）由散點圖可以判斷， 適宜作為年銷售量y關于年宣傳費x的回歸方程類

型。

（II）令，先建立y關于w的線性回歸方程。由于

。

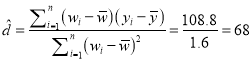
所以y關于w的線性回歸方程為，因此y關于x的回歸方程為

。

（III）（i）由（II）知，當x=49時，年銷售量y的預報值

年利潤z的預報值。

（ii）根據（II）的結果知，年利潤z的預報值

所以當，即x=46.24時， 取得最大值

故年宣傳費為46.24千元時，年利潤的預報值最大。