
【題目】已知集合![]() 若
若
(1)![]() 求實數
求實數![]() 的范圍;
的范圍;
(2)![]() 求實數
求實數![]() 的范圍;
的范圍;
(3)![]() 求實數
求實數![]() 的范圍.
的范圍.
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:高中數學 來源: 題型:
【題目】
問題解決
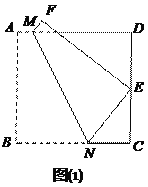
如圖(1),將正方形紙片ABCD折疊,使點B落在CD邊上一點E(不與點C、D重合),壓平后得到折痕MN.當![]() 時,求
時,求![]() 的值.
的值.
類比歸納
在圖(1)中,若![]() 則
則![]() 的值等于 ;若
的值等于 ;若![]() 則
則![]() 的值等于 ;若
的值等于 ;若![]() (n為整數),則
(n為整數),則![]() 的值等于 .(用含
的值等于 .(用含![]() 的式子表示)
的式子表示)
聯系拓廣
如圖(2),將矩形紙片ABCD折疊,使點B落在CD邊上一點E(不與點C、D重合),壓平后得到折痕MN設![]() ,則
,則![]() 的值等
的值等
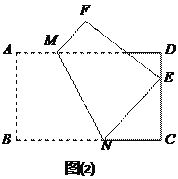
 于 ▲ .(用含
于 ▲ .(用含![]() 的式子表示)
的式子表示)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在高中學習過程中,同學們經常這樣說:“如果物理成績好,那么學習數學就沒什么問題.”某班針對“高中生物理學習對數學學習的影響”進行研究,得到了學生的物理成績與數學成績具有線性相關關系的結論.現從該班隨機抽取5名學生在一次考試中的物理和數學成績,如下表:
編號 成績 | 1 | 2 | 3 | 4 | 5 |
物理( | 90 | 85 | 74 | 68 | 63 |
數學( | 130 | 125 | 110 | 95 | 90 |
求數學成績![]() 關于物理成績
關于物理成績![]() 的線性回歸方程
的線性回歸方程![]() (
(![]() 精確到
精確到![]()
若某位學生的物理成績為80分,預測他的數學成績;
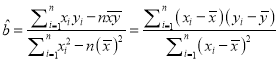
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】公元![]() 年左右,我國數學家劉徽發現當圓內接正多邊形的邊數無限增加時,多邊形的面積可無限逼近圓的面積,并創立了“割圓術”劉徽得到了圓周率精確到小數點后兩位的近似值
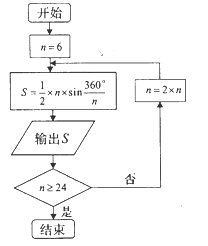
年左右,我國數學家劉徽發現當圓內接正多邊形的邊數無限增加時,多邊形的面積可無限逼近圓的面積,并創立了“割圓術”劉徽得到了圓周率精確到小數點后兩位的近似值![]() ,這就是著名的“徽率”.如圖是利用劉徽的“割圓術”思想設計的一個程序框圖,其中
,這就是著名的“徽率”.如圖是利用劉徽的“割圓術”思想設計的一個程序框圖,其中![]() 表示圓內接正多邊形的邊數,執行此算法輸出的圓周率的近似值依次為 ( )
表示圓內接正多邊形的邊數,執行此算法輸出的圓周率的近似值依次為 ( )
(參考數據: ![]() )
)
A. 2.598,3,3.1048 B. 2.598,3,3.1056
C. 2.578,3,3.1069 D. 2.588,3,3.1108
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,三棱柱![]() 的底面是邊長為2的正三角形且側棱垂直于底面,側棱長是
的底面是邊長為2的正三角形且側棱垂直于底面,側棱長是![]() ,
, ![]() 是
是![]() 的中點.
的中點.

(1)求證: ![]() 平面
平面![]() ;
;
(2)求二面角![]() 的大小;
的大小;
(3)求直線![]() 與平面
與平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】潮州統計局就某地居民的月收入調查了![]() 人,并根據所得數據畫了樣本的頻率分
人,并根據所得數據畫了樣本的頻率分
布直方圖(每個分組包括左端點,不包括右端點,如第一組表示收入在![]() )。
)。

(1)求居民月收入在![]() 的頻率;
的頻率;
(2)根據頻率分布直方圖算出樣本數據的中位數;
(3)為了分析居民的收入與年齡、職業等方面的關系,必須按月收入再從這![]() 人中分層抽樣方法抽出
人中分層抽樣方法抽出![]() 人作進一步分析,則月收入在
人作進一步分析,則月收入在![]() 的這段應抽多少人?
的這段應抽多少人?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】國際奧委會將于2017年9月15日在秘魯利馬召開130次會議決定2024年第33屆奧運會舉辦地。目前德國漢堡、美國波士頓等申辦城市因市民擔心賽事費用超支而相繼退出。某機構為調查我國公民對申辦奧運會的態度,選了某小區的100位居民調查結果統計如下:

(1)根據已有數據,把表格數據填寫完整;
(2)能否在犯錯誤的概率不超過5%的前提下認為不同年齡與支持申辦奧運無關?
(3)已知在被調查的年齡大于50歲的支持者中有5名女性,其中2位是女教師,現從這5名女性中隨機抽取3人,求至多有1位教師的概率.
附:  ,
, ![]() .
.
![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() (
(![]() 為常數,
為常數,![]() =2.71828……是自然對數的底數),曲線
=2.71828……是自然對數的底數),曲線![]() 在點
在點![]() 處的切線與
處的切線與![]() 軸平行.
軸平行.
(1)求![]() 的值;
的值;
(2)求![]() 的單調區間;
的單調區間;
(3)設![]() ,其中
,其中![]() 是
是![]() 的導函數.證明:對任意
的導函數.證明:對任意![]() >0,
>0,![]() <
<![]() .
.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com