【題目】2014年推出一種新型家用轎車，購買時費用為14.4萬元，每年應交付保險費、養路費及汽車油費共0.7萬元，
汽車維修費為：第一年無維修費用，第二年為0.2萬元，從第三年起，每年的維修費用均比上一年增加0.2萬元
（1）設該輛轎車使用n年的總費用（包括購買費用，保險費，養路費，汽車費及維修費）為f（n），求f（n）的表達式．
（2）這種汽車使用多少年報廢最合算（即該車使用多少年，年平均費用最少）？
【答案】
（1）解：由題意得：每年的維修費構成一等差數列，n年的維修總費用為
（萬元）
所以f（n）=14.4+0.7n+（0.1n2﹣0.1n）
=0.1n2+0.6n+14.4（萬元）
（2）解：該輛轎車使用n年的年平均費用為
0.1n+0.6+ 
=3（萬元）
當且僅當 
時取等號，此時n=12
答：這種汽車使用12年報廢最合算
【解析】（1）由已知中某種汽車購買時費用為14.4萬元，每年應交付保險費、養路費及汽油費共0.7萬元，汽車的維修費為：第一年0.2萬元，第二年0.4萬元，第三年0.6萬元，…，依等差數列逐年遞增，根據等差數列前n項和公式，即可得到f（n）的表達式；（2）由（1）中使用n年該車的總費用，得到n年平均費用表達式，根據基本不等式，計算出平均費用最小時的n值，進而得到結論．
科目：高中數學 來源： 題型：
【題目】已知函數f（x）=|x﹣a|．
（1）若f（x）≤m的解集為{x|﹣1≤x≤5}，求實數a，m的值．
（2）當a=2且0≤t＜2時，解關于x的不等式f（x）+t≥f（x+2）．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知向量 
=（cos2x， 
sinx）， 
=（1，cosx），函數f（x）=2 +m，且當x∈[0， 
]時，f（x）的最小值為2．
（1）求m的值，并求f（x）圖象的對稱軸方程；
（2）設函數g（x）=[f（x）2]﹣f（x），x∈[0， ]，求g（x）的最大值．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖，已知橢圓
，點B是其下頂點，過點B的直線交橢圓C于另一點A（A點在
軸下方），且線段AB的中點E在直線
上.
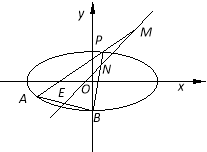
（1）求直線AB的方程；
（2）若點P為橢圓C上異于A、B的動點，且直線AP,BP分別交直線
于點M、N，證明：OM·ON為定值.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】（本題滿分16分）已知函數
， 
．
（1）若函數
在
上單調遞增，求實數
的取值范圍；
（2）若直線
是函數
圖象的切線，求
的最小值；
（3）當
時，若
與
的圖象有兩個交點
，求證： 
．（取
為
，取
為
，取
為
）
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知函數f（x）=2asinωxcosωx+2 
cos2ωx﹣ +1（a＞0，ω＞0）的最大值為3，最小正周期為π．
（1）求函數f（x）的單調遞增區間．
（2）若f（θ）= 
，求sin（4θ+ 
）的值．
（3）若存在區間[a，b]（a，b∈R，且a＜b）使得y=f（x）在[a，b]上至少含有6個零點，在滿足上述條件的[a，b]中，求b﹣a的最小值．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】在△ABC中，角A、B、C對邊分別為a、b、c，sinA+sinB=2sinC，a=2b．
（1）證明：△ABC為鈍角三角形；
（2）若S△ABC= 
，求c．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
