
【題目】5G網絡是第五代移動通信網絡,其峰值理論傳輸速度可達每8秒1GB,比4G網絡的傳輸速度快數百倍.舉例來說,一部1G的電影可在8秒之內下載完成.隨著5G技術的誕生,用智能終端分享3D電影、游戲以及超高畫質(UHD)節目的時代正向我們走來.某手機網絡研發公司成立一個專業技術研發團隊解決各種技術問題,其中有數學專業畢業,物理專業畢業,其它專業畢業的各類研發人員共計1200人.現在公司為提高研發水平,采用分層抽樣抽取400人按分數對工作成績進行考核,并整理得如上頻率分布直方圖(每組的頻率視為概率).

(1)從總體的1200名學生中隨機抽取1人,估計其分數小于50的概率;
(2)研發公司決定對達到某分數以上的研發人員進行獎勵,要求獎勵研發人員的人數達到30%,請你估計這個分數的值;
(3)已知樣本中有三分之二的數學專業畢業的研發人員分數不低于70分,樣本中不低于70分的數學專業畢業的研發人員人數與物理及其它專業畢業的研發人員的人數和相等,估計總體中數學專業畢業的研發人員的人數.
【答案】(1)0.1;(2)77.5;(3)540人.
【解析】
(1)由題意可知,樣本中隨機抽取一人,分數小于50的概率是0.1,由此能估計總體中分數小于50的概率;
(2)根據頻率分布直方圖,第六組的頻率為0.4,第七組頻率為0.2,由此能求出這個分數;
(3)樣本中不低于70分的研發人員人數為240人,從而樣本中不低于70分的數學專業畢業的研發人員為120人,樣本中有三分之二的數學專業畢業的研發人員分數不低于70分,從而樣本中的是數學專業畢業的研發人員的人數為180人,由此能估計總體中數學專業畢業的研發人員的人數
解:(1)由題意可知,樣本中隨機抽取一人,
分數小于50的概率是![]() ,
,
所以估計總體中分數小于50的概率0.1
(2)根據頻率分布直方圖,
第六組的頻率為0.04×10=0.4,第七組頻率為0.02×10=0.2,
此分數為![]()
(3)因為樣本中不低于70分的研發人員人數為400×(0.4+0.2)=240人,
所以樣本中不低于70分的數學專業畢業的研發人員為120人,
又因為樣本中有三分之二的數學專業畢業的研發人員分數不低于70分,
所以樣本中的是數學專業畢業的研發人員的人數120÷![]() =180人,
=180人,
故估計總體中數學專業畢業的研發人員的人數為:1200×![]() =540人
=540人


科目:高中數學 來源: 題型:
【題目】
如圖,在三棱錐P—ABC中,PC⊥底面ABC,AB⊥BC,D,E分別是AB,PB的中點.

(Ⅰ)求證:DE∥平面PAC.
(Ⅱ)求證:AB⊥PB;
(Ⅲ)若PC=BC,求二面角P—AB—C的大小.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設函數![]() ,
,![]() ,且對所有的實數
,且對所有的實數![]() ,等式
,等式![]() 都成立,其
都成立,其![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() ,
,![]() 、
、![]() .
.
(1)如果函數![]() ,
,![]() ,求實數
,求實數![]() 的值;
的值;
(2)設函數![]() ,直接寫出滿足
,直接寫出滿足![]() 的兩個函數
的兩個函數![]() ;
;
(3)如果方程![]() 無實數解,求證:方程
無實數解,求證:方程![]() 無實解.
無實解.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() :
: ![]() 的左右焦點分別為
的左右焦點分別為![]() ,
, ![]() ,左頂點為
,左頂點為![]() ,上頂點為
,上頂點為![]() ,
, ![]() 的面積為
的面積為![]() .
.
(1)求橢圓![]() 的方程;
的方程;
(2)設直線![]() :
: ![]() 與橢圓
與橢圓![]() 相交于不同的兩點
相交于不同的兩點![]() ,
, ![]() ,
, ![]() 是線段
是線段![]() 的中點.若經過點
的中點.若經過點![]() 的直線
的直線![]() 與直線
與直線![]() 垂直于點
垂直于點![]() ,求
,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在直角坐標系![]() 中,曲線
中,曲線![]() 的參數方程為
的參數方程為![]() (
(![]() 為參數),直線
為參數),直線![]() 的參數方程為
的參數方程為![]() (
(![]() 為參數).
為參數).
(Ⅰ)若![]() ,求直線
,求直線![]() 被曲線
被曲線![]() 截得的線段的長度;
截得的線段的長度;
(Ⅱ)若![]() ,在曲線
,在曲線![]() 上求一點
上求一點![]() ,使得點
,使得點![]() 到直線
到直線![]() 的距離最小,并求出最小距離.
的距離最小,并求出最小距離.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】從某居民區隨機抽取10個家庭,獲得第![]() 個家庭的月收入
個家庭的月收入![]() (單位:千元)與月儲蓄
(單位:千元)與月儲蓄![]() (單位:千元)的數據資料,算得
(單位:千元)的數據資料,算得![]() ,
, ![]() ,
,
![]() ,
, ![]()
(1).求家庭的月儲蓄![]() 對月收入
對月收入![]() 的線性回歸方程
的線性回歸方程![]() ;
;
(2).判斷變量![]() 與
與![]() 之間的正相關還是負相關;
之間的正相關還是負相關;
(3).若該居民區某家庭月收入為7千元,預測該家庭的月儲蓄.
附:回歸直線的斜率和截距的最小二乘估計公式分別為
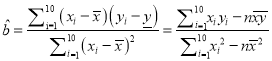
![]()
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com