
【題目】已知橢圓![]() :
: ![]() 的左右焦點分別為
的左右焦點分別為![]() ,
, ![]() ,左頂點為
,左頂點為![]() ,上頂點為
,上頂點為![]() ,
, ![]() 的面積為
的面積為![]() .
.
(1)求橢圓![]() 的方程;
的方程;
(2)設直線![]() :
: ![]() 與橢圓
與橢圓![]() 相交于不同的兩點
相交于不同的兩點![]() ,
, ![]() ,
, ![]() 是線段
是線段![]() 的中點.若經過點
的中點.若經過點![]() 的直線
的直線![]() 與直線
與直線![]() 垂直于點
垂直于點![]() ,求
,求![]() 的取值范圍.
的取值范圍.
科目:高中數學 來源: 題型:
【題目】袋子中放有大小和形狀相同的小球若干個,其中標號為0的小球1個,標號為1的小球1個,標號為2的小球n個.已知從袋子中隨機抽取1個小球,取到標號是2的小球的概率是![]() .
.
(1)求n的值;
(2)從袋子中不放回地隨機抽取2個小球,記第一次取出的小球標號為a,第二次取出的小球標號為b.
①記事件A表示“a+b=2”,求事件A的概率;
②在區間[0,2]內任取2個實數x,y,求事件“x2+y2>(a-b)2恒成立”的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓C的中心在原點,焦點F1 , F2在軸上,焦距為2,離心率為 ![]() .
.
(1)求橢圓C的方程;
(2)若P是橢圓C上第一象限內的點,△PF1F2的內切圓的圓心為I,半徑為 ![]() .求:
.求:
(i)點P的坐標;
(ii)直線PI的方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在四棱錐P﹣ABCD中,底面ABCD是正方形,側棱PD⊥底面ABCD,PD=DC=2,E是PC的中點. 
(1)求證:PA∥平面EDB;
(2)求銳二面角C﹣PB﹣D的大小.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】隨著我國經濟的發展,居民的儲蓄存款逐年增長.設某地區城鄉居民人民幣儲蓄存款(年底余額)如下表:
年份 | 2010 | 2011 | 2012 | 2013 | 2014 |
時間代號 | 1 | 2 | 3 | 4 | 5 |
儲蓄存款 | 6 | 7 | 8 | 9 | 10 |
(1)求![]() 關于
關于![]() 的回歸方程
的回歸方程![]() ;
;
(2)用所求回歸方程預測該地區2015年![]() 的人民幣儲蓄存款.
的人民幣儲蓄存款.
附:回歸方程![]() 中,
中, 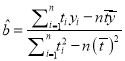 ,
,
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】規定記號“*”表示一種運算,a*b=a2+ab,設函數f(x)=x*2,且關于x的方程f(x)=ln|x+1|(x≠﹣1)恰有4個互不相等的實數根x1 , x2 , x3 , x4 , 則x1+x2+x3+x4= .
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com