
【題目】設函數![]() ,
,![]() ,且對所有的實數
,且對所有的實數![]() ,等式
,等式![]() 都成立,其
都成立,其![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() ,
,![]() 、
、![]() .
.
(1)如果函數![]() ,
,![]() ,求實數
,求實數![]() 的值;
的值;
(2)設函數![]() ,直接寫出滿足
,直接寫出滿足![]() 的兩個函數
的兩個函數![]() ;
;
(3)如果方程![]() 無實數解,求證:方程
無實數解,求證:方程![]() 無實解.
無實解.
科目:高中數學 來源: 題型:
【題目】原命題:“![]() ,
, ![]() 為兩個實數,若
為兩個實數,若![]() ,則
,則![]() ,
, ![]() 中至少有一個不小于1”,下列說法錯誤的是( )
中至少有一個不小于1”,下列說法錯誤的是( )
A. 逆命題為:若![]() ,
, ![]() 中至少有一個不小于1,則
中至少有一個不小于1,則![]() ,為假命題
,為假命題
B. 否命題為:若![]() ,則
,則![]() ,
, ![]() 都小于1,為假命題
都小于1,為假命題
C. 逆否命題為:若![]() ,
, ![]() 都小于1,則
都小于1,則![]() ,為真命題
,為真命題
D. “![]() ”是“
”是“![]() ,
, ![]() 中至少有一個不小于1”的必要不充分條件
中至少有一個不小于1”的必要不充分條件
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某工廠為了對新研發的一種產品進行合理定價,將該產品按事先擬定的價格進行試銷,得到如下數據:
單價x(元) | 8 | 8.2 | 8.4 | 8.6 | 8.8 | 9 |
銷量y(件) | 90 | 84 | 83 | 80 | 75 | 68 |
(1)求回歸直線方程![]() =bx+a;(其中
=bx+a;(其中 ,
,![]() ,
,![]() ,
,![]() ,
,![]() );
);
(2)預計在今后的銷售中,銷量與單價仍然服從(1)中的關系,且該產品的成本是4元/件,為使工廠獲得最大利潤,該產品的單價應定為多少元?(利潤=銷售收入-成本)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在四棱錐![]() 中,底面
中,底面![]() 是矩形,
是矩形, ![]() 垂直于底面
垂直于底面![]() ,
, ![]() ,點
,點![]() 為線段
為線段![]() (不含端點)上一點.
(不含端點)上一點.

(1)當![]() 是線段
是線段![]() 的中點時,求
的中點時,求![]() 與平面
與平面![]() 所成角的正弦值;
所成角的正弦值;
(2)已知二面角![]() 的正弦值為
的正弦值為![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知![]() 是數列
是數列![]() 的前n項和,
的前n項和,![]() ,且
,且![]() .
.
(1)求數列![]() 的通項公式;
的通項公式;
(2)對于正整數![]() ,已知
,已知![]() 成等差數列,求正整數
成等差數列,求正整數![]() 的值;
的值;
(3)設數列![]() 前n項和是
前n項和是![]() ,且滿足:對任意的正整數n,都有等式
,且滿足:對任意的正整數n,都有等式![]() 成立.求滿足等式
成立.求滿足等式![]() 的所有正整數n.
的所有正整數n.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖所示,在Rt△ABC中,已知點A(-2,0),直角頂點B(0,-2![]() ),點C在x軸上。
),點C在x軸上。
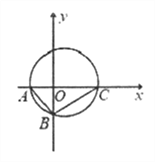
(1)求Rt△ABC外接圓的方程;
(2)求過點(-4,0)且與Rt△ABC外接圓相切的直線的方程。
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】5G網絡是第五代移動通信網絡,其峰值理論傳輸速度可達每8秒1GB,比4G網絡的傳輸速度快數百倍.舉例來說,一部1G的電影可在8秒之內下載完成.隨著5G技術的誕生,用智能終端分享3D電影、游戲以及超高畫質(UHD)節目的時代正向我們走來.某手機網絡研發公司成立一個專業技術研發團隊解決各種技術問題,其中有數學專業畢業,物理專業畢業,其它專業畢業的各類研發人員共計1200人.現在公司為提高研發水平,采用分層抽樣抽取400人按分數對工作成績進行考核,并整理得如上頻率分布直方圖(每組的頻率視為概率).

(1)從總體的1200名學生中隨機抽取1人,估計其分數小于50的概率;
(2)研發公司決定對達到某分數以上的研發人員進行獎勵,要求獎勵研發人員的人數達到30%,請你估計這個分數的值;
(3)已知樣本中有三分之二的數學專業畢業的研發人員分數不低于70分,樣本中不低于70分的數學專業畢業的研發人員人數與物理及其它專業畢業的研發人員的人數和相等,估計總體中數學專業畢業的研發人員的人數.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,天津之眼,全稱天津永樂橋摩天輪,是世界上唯一一個橋上瞰景摩天輪,是天津的地標之一 .永樂橋分上下兩層,上層橋面預留了一個長方形開口,供摩天輪輪盤穿過,摩天輪的直徑為110米,外掛裝48個透明座艙,在電力的驅動下逆時針勻速旋轉,轉一圈大約需要30分鐘.現將某一個透明座艙視為摩天輪上的一個點![]() ,當點
,當點![]() 到達最高點時,距離下層橋面的高度為113米,點
到達最高點時,距離下層橋面的高度為113米,點![]() 在最低點處開始計時.
在最低點處開始計時.

(1)試確定在時刻![]() (單位:分鐘)時點
(單位:分鐘)時點![]() 距離下層橋面的高度
距離下層橋面的高度![]() (單位:米);
(單位:米);
(2)若轉動一周內某一個摩天輪透明座艙在上下兩層橋面之間的運行時間大約為5分鐘,問上層橋面距離下層橋面的高度約為多少米?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】平面四邊形![]() 中,
中, ![]() ,
, ![]() 為等邊三角形,現將
為等邊三角形,現將![]() 沿
沿![]() 翻折得到四面體
翻折得到四面體![]() ,點
,點![]() 分別為
分別為![]() 的中點.
的中點.


(Ⅰ)求證:四邊形![]() 為矩形;
為矩形;
(Ⅱ)當平面![]() 平面
平面![]() 時,求直線
時,求直線![]() 與平面
與平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com