
【題目】有甲、乙兩種商品,經銷這兩種商品所能獲得的利潤分別是p萬元和q萬元.它們與投入資金x萬元的關系是:p= ![]() x,q=
x,q= ![]() .今有3萬元資金投入經營這兩種商品,為獲得最大利潤,對這兩種商品的資金分別投入多少時,能獲取最大利潤?最大利潤為多少?
.今有3萬元資金投入經營這兩種商品,為獲得最大利潤,對這兩種商品的資金分別投入多少時,能獲取最大利潤?最大利潤為多少?
【答案】解:設對乙商品投入資金x萬元,則對甲投入資金為(3﹣x)萬元,此時獲取利潤為y萬元;
則由題意知, ![]() .
.
令 ![]() ,則y=﹣
,則y=﹣ ![]() t2+
t2+ ![]() t+
t+ ![]() =
= ![]() (其中0≤t≤
(其中0≤t≤ ![]() );
);
根據二次函數的圖象與性質知,當t= ![]() 時,y有最大值,為
時,y有最大值,為 ![]() ;
;
又t= ![]() ,得
,得 ![]() =
= ![]() ,∴x=
,∴x= ![]() =2.25(萬元),∴3﹣x=0.75(萬元);
=2.25(萬元),∴3﹣x=0.75(萬元);
所以,對甲投入資金0.75萬元,對乙投資2.25萬元時,獲取利潤最大,為 ![]() 萬元
萬元
【解析】如果設對乙商品投入資金x萬元,則對甲投入資金為(3﹣x)萬元,獲取的利潤為y萬元;那么y=p+q,代入可得關于x的解析式,利用換元法得到二次函數f(t),再由二次函數的圖象與性質,求導y的最大值,和對應的t、x.


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:
【題目】設f(n)=(1+ ![]() )n﹣n,其中n為正整數.
)n﹣n,其中n為正整數.
(1)求f(1),f(2),f(3)的值;
(2)猜想滿足不等式f(n)<0的正整數n的范圍,并用數學歸納法證明你的猜想.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在海岸線![]() 一側
一側![]() 處有一個美麗的小島,某旅游公司為方便游客,在
處有一個美麗的小島,某旅游公司為方便游客,在![]() 上設立了
上設立了![]() 兩個報名點,滿足
兩個報名點,滿足![]() 中任意兩點間的距離為
中任意兩點間的距離為![]() .公司擬按以下思路運作:先將
.公司擬按以下思路運作:先將![]() 兩處游客分別乘車集中到
兩處游客分別乘車集中到![]() 之間的中轉點
之間的中轉點![]() 處(點
處(點![]() 異于
異于![]() 兩點),然后乘同一艘輪游輪前往
兩點),然后乘同一艘輪游輪前往![]() 島.據統計,每批游客
島.據統計,每批游客![]() 處需發車2輛,
處需發車2輛, ![]() 處需發車4輛,每輛汽車每千米耗費
處需發車4輛,每輛汽車每千米耗費![]() 元,游輪每千米耗費
元,游輪每千米耗費![]() 元.(其中
元.(其中![]() 是正常數)設∠
是正常數)設∠![]() ,每批游客從各自報名點到
,每批游客從各自報名點到![]() 島所需運輸成本為
島所需運輸成本為![]() 元.
元.
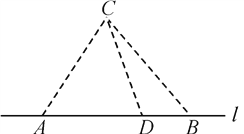
(1) 寫出![]() 關于
關于![]() 的函數表達式,并指出
的函數表達式,并指出![]() 的取值范圍;
的取值范圍;
(2) 問:中轉點![]() 距離
距離![]() 處多遠時,
處多遠時, ![]() 最小?
最小?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=2 ![]() sin(x+
sin(x+ ![]() )cos(x+
)cos(x+ ![]() )+sin2x+a的最大值為1.
)+sin2x+a的最大值為1.
(1)求函數f(x)的單調遞增區間;
(2)將f(x)的圖象向左平移 ![]() 個單位,得到函數g(x)的圖象,若方程g(x)=m在x∈[0,
個單位,得到函數g(x)的圖象,若方程g(x)=m在x∈[0, ![]() ]上有解,求實數m的取值范圍.
]上有解,求實數m的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設f(x)=x2+bx+c且f(0)=f(2),則( )
A.f(﹣2)<f(0)<f( ![]() )
)
B.f( ![]() )<f(0)<f(﹣2)??
)<f(0)<f(﹣2)??
C.f( ![]() )<f(﹣2)<f(0)
)<f(﹣2)<f(0)
D.f(0)<f( ![]() )<f(﹣2)
)<f(﹣2)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在四邊形ABCD中,已知 ![]() ∥
∥ ![]() ,
, ![]() =(6,1),
=(6,1), ![]() =(x,y),
=(x,y), ![]() =(﹣2,﹣3).
=(﹣2,﹣3).
(1)求用x表示y的關系式;
(2)若 ![]() ⊥
⊥ ![]() ,求x、y值.
,求x、y值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在平面直角坐標系xOy中,已知橢圓 ![]() =1(a>b>0)的離心率為
=1(a>b>0)的離心率為 ![]() .A為橢圓上異于頂點的一點,點P滿足
.A為橢圓上異于頂點的一點,點P滿足 ![]() =
= ![]() ,
, 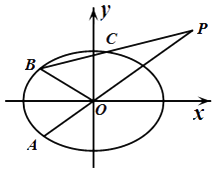
(1)若點P的坐標為(2, ![]() ),求橢圓的方程;
),求橢圓的方程;
(2)設過點P的一條直線交橢圓于B,C兩點,且 ![]() =m
=m ![]() ,直線OA,OB的斜率之積﹣
,直線OA,OB的斜率之積﹣ ![]() ,求實數m的值;
,求實數m的值;
(3)在(1)的條件下,是否存在定圓M,使得過圓M上任意一點T都能作出該橢圓的兩條切線,且這兩條切線互相垂直?若存在,求出定圓M;若不存在,說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com