【題目】在四邊形ABCD中，已知 
∥ 
， 
=（6，1）， =（x，y）， 
=（﹣2，﹣3）．
（1）求用x表示y的關系式；
（2）若 
⊥ 
，求x、y值．
【答案】
（1）解：∵ 
=（6，1）， 
=（x，y）， 
=（﹣2，﹣3），
∴ 
∵ 
，
∴x（﹣2+y）=y（4+x）
∴y=﹣ 
（2）解：∵ =（6，1）， =（x，y）， =（﹣2，﹣3），
∴ 
=（x+6，y+1），
=（x﹣2，y﹣3），
∵ 
，
∴（x+6）（x﹣2）+（y+1）（y﹣3）=0，
又∵y=﹣ ，
解得 
或 
【解析】（1） ，由 ，能求出y=﹣ ．（2） =（x+6，y+1）， =（x﹣2，y﹣3），由 ，y=﹣ ，能求出x、y值．
【考點精析】掌握數量積判斷兩個平面向量的垂直關系是解答本題的根本，需要知道若平面
的法向量為
，平面
的法向量為
，要證
，只需證
，即證
;即：兩平面垂直
兩平面的法向量垂直．
科目：高中數學 來源： 題型：
【題目】如圖，正方形ABCD的邊長為1，P，Q分別為AB，DA上動點，且△APQ的周長為2，設 AP=x，AQ=y．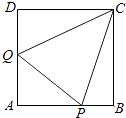 
（1）求x，y之間的函數關系式y=f（x）；
（2）判斷∠PCQ的大小是否為定值？并說明理由；
（3）設△PCQ的面積分別為S，求S的最小值．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】有甲、乙兩種商品，經銷這兩種商品所能獲得的利潤分別是p萬元和q萬元．它們與投入資金x萬元的關系是：p= 
x，q= 
．今有3萬元資金投入經營這兩種商品，為獲得最大利潤，對這兩種商品的資金分別投入多少時，能獲取最大利潤？最大利潤為多少？
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】設集合A={x|2﹣5≤2﹣x≤4}，B={x|x2+2mx﹣3m2＜0，m＞0}．
（1）若m=2，求A∩B；
（2）若BA，求實數m的取值范圍．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知函數y=f（x）滿足以下條件：①定義在正實數集上；②f（ 
）=2；③對任意實數t，都有f（xt）=tf（x）（x∈R+）．
（1）求f（1），f（ 
）的值；
（2）求證：對于任意x，y∈R+ ， 都有f（xy）=f（x）+f（y）；
（3）若不等式f（loga（x﹣3a）﹣1）﹣f（﹣ 
）≥﹣4對x∈[a+2，a+ 
]恒成立，求實數a的取值范圍．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知矩形ABCD的長AB=4，寬AD=3，將其沿對角線BD折起，得到四面體A﹣BCD，如圖所示，給出下列結論：
①四面體A﹣BCD體積的最大值為 
；
②四面體A﹣BCD外接球的表面積恒為定值；
③若E、F分別為棱AC、BD的中點，則恒有EF⊥AC且EF⊥BD；
④當二面角A﹣BD﹣C為直二面角時，直線AB、CD所成角的余弦值為 
；
⑤當二面角A﹣BD﹣C的大小為60°時，棱AC的長為 
．
其中正確的結論有（請寫出所有正確結論的序號）．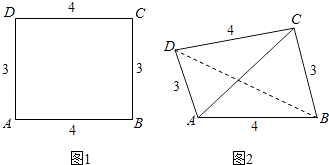
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】為了迎接青奧會，南京將在主干道統一安裝某種新型節能路燈，該路燈由燈柱和支架組成．在如圖所示的直角坐標系中，支架ACB是拋物線y2=2x的一部分，燈柱CD經過該拋物線的焦點F且與路面垂直，其中C在拋物線上，B為拋物線的頂點，DH表示道路路面，BF∥DH，A為錐形燈罩的頂，燈罩軸線與拋物線在A處的切線垂直．安裝時要求錐形燈罩的頂到燈柱的距離是1.5米，燈罩的軸線正好通過道路路面的中線．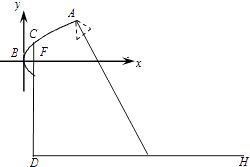 
（1）求燈罩軸線所在的直線方程；
（2）若路寬為10米，求燈柱的高．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖，已知直線與拋物線y2=2px（p＞0）交于A，B兩點，且OA⊥OB，OD⊥AB交AB于點D（不為原點）．
（Ⅰ）求點D的軌跡方程；
（Ⅱ）若點D坐標為（2，1），求p的值．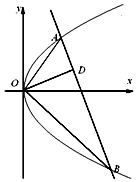
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
