
【題目】中國歷法推測遵循以測為輔、以算為主的原則.例如《周髀算經》和《易經》里對二十四節氣的晷(guǐ)影長的記錄中,冬至和夏至的晷影長是實測得到的,其它節氣的晷影長則是按照等差數列的規律計算得出的.下表為《周髀算經》對二十四節氣晷影長的記錄,其中![]() 寸表示115寸
寸表示115寸![]() 分(1寸=10分).
分(1寸=10分).
節氣 | 冬至 | 小寒(大雪) | 大寒(小雪) | 立春(立冬) | 雨水(霜降) |
晷影長(寸) | 135 |
|
|
|
|
節氣 | 驚蟄(寒露) | 春分(秋分) | 清明(白露) | 谷雨(處暑) | 立夏(立秋) |
晷影長(寸) |
| 75.5 |
|
|
|
節氣 | 小滿(大暑) | 芒種(小暑) | 夏至 | ||
晷影長(寸) |
|
| 16.0 |
已知《易經》中記錄的冬至晷影長為130.0寸,春分晷影長為72.4寸,那么《易經》中所記錄的夏至的晷影長應為( )
A. 14.8寸B. 15.8寸C. 16.0寸D. 18.4寸
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:高中數學 來源: 題型:
【題目】某校學生社團組織活動豐富,學生會為了解同學對社團活動的滿意程度,隨機選取了100位同學進行問卷調查,并將問卷中的這100人根據其滿意度評分值(百分制)按照[40,50),[50,60),[60,70),…,[90,100]分成6組,制成如圖所示頻率分布直方圖.
(1)求圖中x的值;
(2)求這組數據的中位數;
(3)現從被調查的問卷滿意度評分值在[60,80)的學生中按分層抽樣的方法抽取5人進行座談了解,再從這5人中隨機抽取2人作主題發言,求抽取的2人恰在同一組的概率.

查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() ,
,![]() 的圖象與直線
的圖象與直線![]() 分別交于
分別交于![]() 、
、![]() 兩點,則( )
兩點,則( )
A.![]() 的最小值為
的最小值為![]()
B.![]() 使得曲線
使得曲線![]() 在
在![]() 處的切線平行于曲線
處的切線平行于曲線![]() 在
在![]() 處的切線
處的切線
C.函數![]() 至少存在一個零點
至少存在一個零點
D.![]() 使得曲線
使得曲線![]() 在點
在點![]() 處的切線也是曲線
處的切線也是曲線![]() 的切線
的切線
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知曲線![]() 上動點
上動點![]() 與定點
與定點![]() 的距離和它到定直線
的距離和它到定直線![]() 的距離的比是常數
的距離的比是常數![]() .若過
.若過![]() 的動直線
的動直線![]() 與曲線
與曲線![]() 相交于
相交于![]() 兩點.
兩點.
(1)判斷曲線![]() 的名稱并寫出它的標準方程;
的名稱并寫出它的標準方程;
(2)是否存在與點![]() 不同的定點
不同的定點![]() ,使得
,使得![]() 恒成立?若存在,求出點
恒成立?若存在,求出點![]() 的坐標;若不存在,請說明理由。
的坐標;若不存在,請說明理由。
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】今年入冬以來,我市天氣反復.在下圖中統計了我市上個月前15天的氣溫,以及相對去年同期的氣溫差(今年氣溫-去年氣溫,單位:攝氏度),以下判斷錯誤的是( )
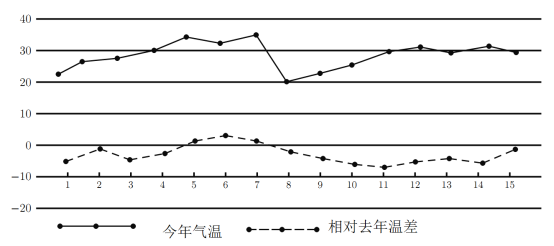
A.今年每天氣溫都比去年氣溫低B.今年的氣溫的平均值比去年低
C.今年8-12號氣溫持續上升D.今年8號氣溫最低
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知![]() 為坐標原點,點
為坐標原點,點![]() ,
,![]() ,
,![]() ,動點
,動點![]() 滿足
滿足![]() ,點
,點![]() 為線段
為線段![]() 的中點,拋物線
的中點,拋物線![]() :
:![]() 上點
上點![]() 的縱坐標為
的縱坐標為![]() ,
,![]() .
.
(1)求動點![]() 的軌跡曲線
的軌跡曲線![]() 的標準方程及拋物線
的標準方程及拋物線![]() 的標準方程;
的標準方程;
(2)若拋物線![]() 的準線上一點
的準線上一點![]() 滿足
滿足![]() ,試判斷
,試判斷![]() 是否為定值,若是,求這個定值;若不是,請說明理由.
是否為定值,若是,求這個定值;若不是,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知平面直角坐標系![]() ,直線
,直線![]() 過點
過點![]() ,且傾斜角為
,且傾斜角為![]() ,以
,以![]() 為極點,
為極點,![]() 軸的非負半軸為極軸建立極坐標系,圓
軸的非負半軸為極軸建立極坐標系,圓![]() 的極坐標方程為
的極坐標方程為![]() .
.
(1)求直線![]() 的參數方程和圓
的參數方程和圓![]() 的標準方程;
的標準方程;
(2)設直線![]() 與圓
與圓![]() 交于
交于![]() 、
、![]() 兩點,若
兩點,若![]() ,求直線
,求直線![]() 的傾斜角的
的傾斜角的![]() 值.
值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com