
【題目】直線l過點M(﹣1,2)且與以P(﹣2,﹣3),Q(4,0)為端點的線段PQ相交,則l的斜率的取值范圍是( )
A.[﹣ ![]() ,5]
,5]
B.[﹣ ![]() ,0)∪(0,5]
,0)∪(0,5]
C.[﹣ ![]() ,
, ![]() )∪(
)∪( ![]() ,5]
,5]
D.(﹣∞,﹣ ![]() ]∪[5,+∞)
]∪[5,+∞)
 亮點激活精編提優100分大試卷系列答案
亮點激活精編提優100分大試卷系列答案 智趣寒假作業云南科技出版社系列答案
智趣寒假作業云南科技出版社系列答案科目:高中數學 來源: 題型:
【題目】已知數列{an}是公差為2的等差數列,且a1 , a4 , a13成等比數列,數列{ ![]() }是首項為1,公比為3的等比數列.
}是首項為1,公比為3的等比數列.
(1)求數列{an}、{bn}的通項公式;
(2)設數列{an+bn}的前n項和Rn , 若不等式 ![]() ≤λ3n+n+3對n∈N*恒成立,求λ的取值范圍.
≤λ3n+n+3對n∈N*恒成立,求λ的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某校從參加高一年級期末考試的學生中抽出40名學生,將其成績(均為整數)分成六段![]() 后畫出如下部分頻率分布直方圖,觀察圖形的信息,回答下列問題:
后畫出如下部分頻率分布直方圖,觀察圖形的信息,回答下列問題:

(1)求第四小組的頻率,并補全頻率分布直方圖;
(2)估計這次考試的及格率(60分及以上為及格)和平均分;
(3)從成績是![]() ~
~![]() 分及
分及![]() ~
~![]() 分的學生中選兩人,記他們的成績為
分的學生中選兩人,記他們的成績為![]() ,求滿足“
,求滿足“![]() ”的概率.
”的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某市有![]() 三所高校,其學生會學習部有“干事”人數分別為
三所高校,其學生會學習部有“干事”人數分別為![]() ,現采用分層抽樣的方法從這些“干事”中抽取
,現采用分層抽樣的方法從這些“干事”中抽取![]() 名進行“大學生學習部活動現狀”調查.
名進行“大學生學習部活動現狀”調查.
(1)求應從![]() 這三所高校中分別抽取的“干事”人數;
這三所高校中分別抽取的“干事”人數;
(2)若從抽取的![]() 名干事中隨機選兩名干事,求選出的
名干事中隨機選兩名干事,求選出的![]() 名干事來自同一所高校的概率.
名干事來自同一所高校的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某地區擬建立一個藝術博物館,采取競標的方式從多家建筑公司選取一家建筑公司,經過層層篩選,甲、乙兩家建筑公司進入最后的招標.現從建筑設計院聘請專家設計了一個招標方案:兩家公司從![]() 個招標問題中隨機抽取
個招標問題中隨機抽取![]() 個問題,已知這
個問題,已知這![]() 個招標問題中,甲公司可正確回答其中的
個招標問題中,甲公司可正確回答其中的![]() 道題目,而乙公司能正確回答毎道題目的概率均為
道題目,而乙公司能正確回答毎道題目的概率均為![]() ,甲、乙兩家公司對每題的回答都是相互獨立,互不影響的.
,甲、乙兩家公司對每題的回答都是相互獨立,互不影響的.
(1)求甲、乙兩家公司共答對![]() 道題目的概率;
道題目的概率;
(2)請從期望和方差的角度分析,甲、乙兩家哪家公司競標成功的可能性更大?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知圓C:x2+y2+2x-4y+3=0.
(1)若圓C的切線在x軸和y軸上的截距相等,求此切線的方程.
(2)從圓C外一點P(x1,y1)向該圓引一條切線,切點為M,O為坐標原點,且有|PM|=|PO|,求使得|PM|取得最小值的點P的坐標.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知數列{an}的首項為a1= ![]() ,且2an+1=an(n∈N+).
,且2an+1=an(n∈N+).
(1)求{an}的通項公式;
(2)若數列{bn}滿足bn= ![]() ,求{bn}的前n項和Tn .
,求{bn}的前n項和Tn .
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】【2016高考浙江理數】如圖,設橢圓![]() (a>1).
(a>1).
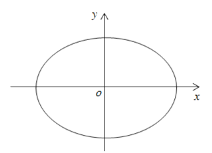
(I)求直線y=kx+1被橢圓截得的線段長(用a、k表示);
(II)若任意以點A(0,1)為圓心的圓與橢圓至多有3個公共點,求橢圓離心率的取值
范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com