
【題目】【2016高考浙江理數(shù)】如圖,設(shè)橢圓![]() (a>1).
(a>1).
(I)求直線y=kx+1被橢圓截得的線段長(用a、k表示);
(II)若任意以點A(0,1)為圓心的圓與橢圓至多有3個公共點,求橢圓離心率的取值
范圍.
【答案】(I)![]() ;(II)
;(II)![]() .
.
【解析】
試題分析:(I)先聯(lián)立![]() 和
和![]() ,可得
,可得![]() ,
,![]() ,再利用弦長公式可得直線
,再利用弦長公式可得直線![]() 被橢圓截得的線段長;(II)先假設(shè)圓與橢圓的公共點有
被橢圓截得的線段長;(II)先假設(shè)圓與橢圓的公共點有![]() 個,再利用對稱性及已知條件可得任意以點
個,再利用對稱性及已知條件可得任意以點![]() 為圓心的圓與橢圓至多有
為圓心的圓與橢圓至多有![]() 個公共點時,
個公共點時,![]() 的取值范圍,進而可得橢圓離心率的取值范圍.
的取值范圍,進而可得橢圓離心率的取值范圍.
試題解析:(I)設(shè)直線![]() 被橢圓截得的線段為
被橢圓截得的線段為![]() ,由
,由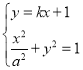 得
得
![]() ,故
,故![]() ,
,![]() .
.
因此![]() .
.
(II)假設(shè)圓與橢圓的公共點有![]() 個,由對稱性可設(shè)
個,由對稱性可設(shè)![]() 軸左側(cè)的橢圓上有兩個不同的點
軸左側(cè)的橢圓上有兩個不同的點![]() ,
,![]() ,滿足
,滿足
![]() .
.
記直線![]() ,
,![]() 的斜率分別為
的斜率分別為![]() ,
,![]() ,且
,且![]() ,
,![]() ,
,![]() .
.
由(I)知,
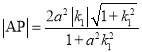 ,
,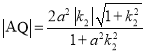 ,
,
故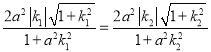 ,
,
所以![]() .
.
由于![]() ,
,![]() ,
,![]() 得
得
![]() ,
,
因此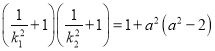 , ①
, ①
因為①式關(guān)于![]() ,
,![]() 的方程有解的充要條件是
的方程有解的充要條件是![]() ,所以
,所以![]() .
.
因此,任意以點![]() 為圓心的圓與橢圓至多有
為圓心的圓與橢圓至多有![]() 個公共點的充要條件為
個公共點的充要條件為![]() ,
,
由![]() 得,所求離心率的取值范圍為
得,所求離心率的取值范圍為![]() .
.


科目:高中數(shù)學 來源: 題型:
【題目】直線l過點M(﹣1,2)且與以P(﹣2,﹣3),Q(4,0)為端點的線段PQ相交,則l的斜率的取值范圍是( )
A.[﹣ ![]() ,5]
,5]
B.[﹣ ![]() ,0)∪(0,5]
,0)∪(0,5]
C.[﹣ ![]() ,
, ![]() )∪(
)∪( ![]() ,5]
,5]
D.(﹣∞,﹣ ![]() ]∪[5,+∞)
]∪[5,+∞)
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知A,B分別是直線y=x和y=﹣x上的兩個動點,線段AB的長為2 ![]() ,D是AB的中點.
,D是AB的中點.
(1)求動點D的軌跡C的方程;
(2)若過點(1,0)的直線l與曲線C交于不同兩點P、Q,
①當|PQ|=3時,求直線l的方程;
②試問在x軸上是否存在點E(m,0),使 ![]()
![]() 恒為定值?若存在,求出E點的坐標及定值;若不存在,請說明理由.
恒為定值?若存在,求出E點的坐標及定值;若不存在,請說明理由.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】運貨卡車以每小時x千米的速度勻速行駛130千米(50≤x≤100)(單位:千米/小時).假設(shè)汽油的價格是每升2元,而汽車每小時耗油(2+ ![]() )升,司機的工資是每小時14元.
)升,司機的工資是每小時14元.
(1)求這次行車總費用y關(guān)于x的表達式;
(2)當x為何值時,這次行車的總費用最低,并求出最低費用的值.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
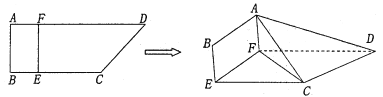
【題目】如圖,四邊形![]() 中,
中, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 分別在
分別在![]() 上,
上, ![]() ,現(xiàn)將四邊形
,現(xiàn)將四邊形![]() 沿
沿![]() 折起,使
折起,使![]() .
.
(1)若![]() ,在折疊后的線段
,在折疊后的線段![]() 上是否存在一點
上是否存在一點![]() ,使得
,使得![]() 平面
平面![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,說明理由;
的值;若不存在,說明理由;
(2)求三棱錐![]() 的體積的最大值,并求出此時點
的體積的最大值,并求出此時點![]() 到平面
到平面![]() 的距離.
的距離.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
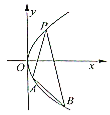
【題目】【廣西名校2017屆高三上學期第一次摸底】如圖,過拋物線![]() 上一點
上一點![]() ,作兩條直線分別交拋物線于
,作兩條直線分別交拋物線于![]() ,
,![]() ,
,
當![]() 與
與![]() 的斜率存在且傾斜角互補時:
的斜率存在且傾斜角互補時:
(Ⅰ)求![]() 的值;
的值;
(Ⅱ)若直線![]() 在
在![]() 軸上的截距
軸上的截距![]() 時,求
時,求![]() 面積
面積![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知點P(x、y)滿足
(1)若x∈{0,1,2,3,4,5},y∈{0,1,2,3,4},則求y≥x的概率.
(2)若x∈[0,5],y∈[0,4],則求x>y的概率.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知{an}為等差數(shù)列,a1+a3+a5=105,a2+a4+a6=99,以Sn表示{an}的前n項和,則使得Sn達到最大值的n是( )
A.21
B.20
C.19
D.18
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com