
【題目】已知函數(shù) ,函數(shù)F(x)=f(x)﹣b有四個(gè)不同的零點(diǎn)x1,x2,x3,x4,且滿(mǎn)足:x1<x2<x3<x4,則
,函數(shù)F(x)=f(x)﹣b有四個(gè)不同的零點(diǎn)x1,x2,x3,x4,且滿(mǎn)足:x1<x2<x3<x4,則![]() 的取值范圍是( )
的取值范圍是( )
A.[![]() ,+∞)B.(3,
,+∞)B.(3,![]() ]C.[3,+∞)D.
]C.[3,+∞)D.![]()
【答案】D
【解析】
函數(shù)![]() 有4個(gè)不同的零點(diǎn)x1,x2,x3,x4,轉(zhuǎn)化為
有4個(gè)不同的零點(diǎn)x1,x2,x3,x4,轉(zhuǎn)化為![]() 有4個(gè)交點(diǎn),結(jié)合函數(shù)
有4個(gè)交點(diǎn),結(jié)合函數(shù)![]() 的圖象得 x1+x2=﹣4,x3x4=1,利用換元法求出新函數(shù)的值域即可.
的圖象得 x1+x2=﹣4,x3x4=1,利用換元法求出新函數(shù)的值域即可.
函數(shù) 圖象如圖所示,函數(shù)F(x)=f(x)﹣b有四個(gè)不同的零點(diǎn)x1,x2,x3,x4,
圖象如圖所示,函數(shù)F(x)=f(x)﹣b有四個(gè)不同的零點(diǎn)x1,x2,x3,x4,
且滿(mǎn)足:x1<x2<x3<x4,轉(zhuǎn)化為![]() 有4個(gè)不同的交點(diǎn),由圖象,結(jié)合已知條件得 x1+x2=﹣4,x3x4=1,0<b≤1,
有4個(gè)不同的交點(diǎn),由圖象,結(jié)合已知條件得 x1+x2=﹣4,x3x4=1,0<b≤1,
解不等式0<﹣log3x≤1得:![]() ≤x3<1,
≤x3<1,![]() ,
,
令t=x32,則![]() ≤t<1,令g(t)=2t+
≤t<1,令g(t)=2t+![]() ,則g(t)在[
,則g(t)在[![]() ,
,![]() ]上單調(diào)遞減,[
]上單調(diào)遞減,[![]() ,1)上是增函數(shù).
,1)上是增函數(shù).
g(![]() )=
)=![]() ,g(
,g(![]() )=
)=![]() ,
,![]() ,∴g(
,∴g(![]() )≤g(t)≤g(
)≤g(t)≤g(![]() ),即
),即![]() ≤2t+
≤2t+![]() ≤
≤![]() .
.
故選:D.



 小學(xué)學(xué)習(xí)好幫手系列答案
小學(xué)學(xué)習(xí)好幫手系列答案 小學(xué)同步三練核心密卷系列答案
小學(xué)同步三練核心密卷系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】
已知函數(shù)![]() ,且
,且![]() 。
。
(I)試用含![]() 的代數(shù)式表示
的代數(shù)式表示![]() ;
;
(Ⅱ)求![]() 的單調(diào)區(qū)間;
的單調(diào)區(qū)間;
(Ⅲ)令![]() ,設(shè)函數(shù)
,設(shè)函數(shù)![]() 在
在![]() 處取得極值,記點(diǎn)
處取得極值,記點(diǎn)![]() ,證明:線段
,證明:線段![]() 與曲線
與曲線![]() 存在異于
存在異于![]() 、
、![]() 的公共點(diǎn)。
的公共點(diǎn)。
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】每年春晚都是萬(wàn)眾矚目的時(shí)刻,這些節(jié)目體現(xiàn)的文化內(nèi)涵、歷史背景等反映了社會(huì)的進(jìn)步.國(guó)家的富強(qiáng),人民生活水平的提高等.某學(xué)校高三年級(jí)主任開(kāi)學(xué)初為了解學(xué)生在看春晚后對(duì)節(jié)目體現(xiàn)的文化內(nèi)涵、歷史背景等是否會(huì)在今年的高考題中體現(xiàn)進(jìn)行過(guò)思考,特地隨機(jī)抽取100名高三學(xué)生(其中文科學(xué)生50,理科學(xué)生50名),進(jìn)行了調(diào)查.統(tǒng)計(jì)數(shù)據(jù)如表所示(不完整):
“思考過(guò)” | “沒(méi)有思考過(guò)” | 總計(jì) | |
文科學(xué)生 | 40 | 10 | |
理科學(xué)生 | 30 | ||
總計(jì) | 100 |
(1)補(bǔ)充完整所給表格,并根據(jù)表格數(shù)據(jù)計(jì)算是否有![]() 的把握認(rèn)為看春晚后會(huì)思考節(jié)目體現(xiàn)的文化內(nèi)涵、歷史背景等與文理科學(xué)生有關(guān);
的把握認(rèn)為看春晚后會(huì)思考節(jié)目體現(xiàn)的文化內(nèi)涵、歷史背景等與文理科學(xué)生有關(guān);
(2)①現(xiàn)從上表的”思考過(guò)”的文理科學(xué)生中按分層抽樣選出7人.再?gòu)倪@7人中隨機(jī)抽取4人,記這4人中“文科學(xué)生”的人數(shù)為![]() ,試求
,試求![]() 的分布列與數(shù)學(xué)期望;
的分布列與數(shù)學(xué)期望;
②現(xiàn)設(shè)計(jì)一份試卷(題目知識(shí)點(diǎn)來(lái)自春晚相關(guān)知識(shí)整合與變化),假設(shè)“思考過(guò)”的學(xué)生及格率為![]() ,“沒(méi)有思考過(guò)”的學(xué)生的及格率為
,“沒(méi)有思考過(guò)”的學(xué)生的及格率為![]() .現(xiàn)從“思考過(guò)”與“沒(méi)有思考過(guò)”的學(xué)生中分別隨機(jī)抽取一名學(xué)生進(jìn)行測(cè)試,求兩人至少有一個(gè)及格的概率.
.現(xiàn)從“思考過(guò)”與“沒(méi)有思考過(guò)”的學(xué)生中分別隨機(jī)抽取一名學(xué)生進(jìn)行測(cè)試,求兩人至少有一個(gè)及格的概率.
附參考公式: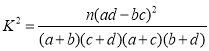 ,其中
,其中![]() .
.
參考數(shù)據(jù):
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖,在四棱錐![]() 中,
中,![]() 平面
平面![]() ,
,![]() ,且
,且![]() ,
,![]() ,
,![]() ,點(diǎn)
,點(diǎn)![]() 在
在![]() 上.
上.
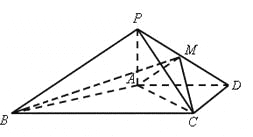
(1)求證:![]() ;
;
(2)若二面角![]() 的大小為
的大小為![]() ,求
,求![]() 與平面
與平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知橢圓![]() 的焦距為4,點(diǎn)P(2,3)在橢圓上.
的焦距為4,點(diǎn)P(2,3)在橢圓上.
(1)求橢圓C的方程;
(2)過(guò)點(diǎn)P引圓![]() 的兩條切線PA,PB,切線PA,PB與橢圓C的另一個(gè)交點(diǎn)分別為A,B,試問(wèn)直線AB的斜率是否為定值?若是,求出其定值,若不是,請(qǐng)說(shuō)明理由.
的兩條切線PA,PB,切線PA,PB與橢圓C的另一個(gè)交點(diǎn)分別為A,B,試問(wèn)直線AB的斜率是否為定值?若是,求出其定值,若不是,請(qǐng)說(shuō)明理由.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知點(diǎn)F1,F(xiàn)2分別為橢圓![]() 的左、右焦點(diǎn),點(diǎn)P為橢圓上任意一點(diǎn),P到焦點(diǎn)F2的距離的最大值為
的左、右焦點(diǎn),點(diǎn)P為橢圓上任意一點(diǎn),P到焦點(diǎn)F2的距離的最大值為![]() ,且△PF1F2的最大面積為1.
,且△PF1F2的最大面積為1.
(Ⅰ)求橢圓C的方程.
(Ⅱ)點(diǎn)M的坐標(biāo)為![]() ,過(guò)點(diǎn)F2且斜率為k的直線L與橢圓C相交于A,B兩點(diǎn).對(duì)于任意的
,過(guò)點(diǎn)F2且斜率為k的直線L與橢圓C相交于A,B兩點(diǎn).對(duì)于任意的![]() 是否為定值?若是求出這個(gè)定值;若不是說(shuō)明理由.
是否為定值?若是求出這個(gè)定值;若不是說(shuō)明理由.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】中國(guó)鐵路總公司相關(guān)負(fù)責(zé)人表示,到2018年底,全國(guó)鐵路營(yíng)業(yè)里程達(dá)到13.1萬(wàn)公里,其中高鐵營(yíng)業(yè)里程2.9萬(wàn)公里,超過(guò)世界高鐵總里程的三分之二,下圖是2014年到2018年鐵路和高鐵運(yùn)營(yíng)里程(單位:萬(wàn)公里)的折線圖,以下結(jié)論不正確的是( )

A.每相鄰兩年相比較,2014年到2015年鐵路運(yùn)營(yíng)里程增加最顯著
B.從2014年到2018年這5年,高鐵運(yùn)營(yíng)里程與年價(jià)正相關(guān)
C.2018年高鐵運(yùn)營(yíng)里程比2014年高鐵運(yùn)營(yíng)里程增長(zhǎng)80%以上
D.從2014年到2018年這5年,高鐵運(yùn)營(yíng)里程數(shù)依次成等差數(shù)列
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】設(shè)函數(shù)![]() 在
在![]() 上有定義,實(shí)數(shù)
上有定義,實(shí)數(shù)![]() 和
和![]() 滿(mǎn)足
滿(mǎn)足![]() ,若
,若![]() 在區(qū)間
在區(qū)間![]() 上不存在最小值,則稱(chēng)
上不存在最小值,則稱(chēng)![]() 在
在![]() 上具有性質(zhì)
上具有性質(zhì)![]() .
.
(1)當(dāng)![]() ,且
,且![]() 在區(qū)間
在區(qū)間![]() 上具有性質(zhì)
上具有性質(zhì)![]() 時(shí),求常數(shù)
時(shí),求常數(shù)![]() 的取值范圍;
的取值范圍;
(2)已知![]() (
(![]() ),且當(dāng)
),且當(dāng)![]() 時(shí),
時(shí),![]() ,判別
,判別![]() 在區(qū)間
在區(qū)間![]() 上是否具有性質(zhì)
上是否具有性質(zhì)![]() ,試說(shuō)明理由.
,試說(shuō)明理由.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖為正方體ABCD-A1B1C1D1,動(dòng)點(diǎn)M從B1點(diǎn)出發(fā),在正方體表面沿逆時(shí)針?lè)较蜻\(yùn)動(dòng)一周后,再回到B1的運(yùn)動(dòng)過(guò)程中,點(diǎn)M與平面A1DC1的距離保持不變,運(yùn)動(dòng)的路程x與l=MA1+MC1+MD之間滿(mǎn)足函數(shù)關(guān)系l=f(x),則此函數(shù)圖象大致是( )
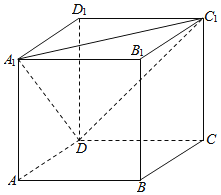
A. 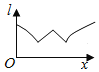 B.
B. 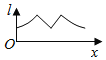
C. 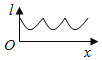 D.
D. 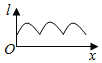
查看答案和解析>>
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專(zhuān)區(qū) | 電信詐騙舉報(bào)專(zhuān)區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專(zhuān)區(qū) | 涉企侵權(quán)舉報(bào)專(zhuān)區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com