
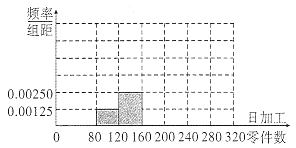
【題目】某大型工廠招聘到一大批新員工.為了解員工對工作的熟練程度,從中隨機抽取100人組成樣本,并統計他們的日加工零件數,得到以下數據;

(1)已知日加工零件數在![]() 范圍內的5名員工中,有3名男工,2名女工,現從中任取兩名進行指導,求他們性別不同的概率;
范圍內的5名員工中,有3名男工,2名女工,現從中任取兩名進行指導,求他們性別不同的概率;
(2)完成頻率分布直方圖,并估計全體新員工每天加工零件數的平均數(每組數據以中點值代替);
 學練快車道快樂假期暑假作業新疆人民出版社系列答案
學練快車道快樂假期暑假作業新疆人民出版社系列答案 浙大優學小學年級銜接導與練浙江大學出版社系列答案
浙大優學小學年級銜接導與練浙江大學出版社系列答案 小學暑假作業東南大學出版社系列答案
小學暑假作業東南大學出版社系列答案 津橋教育暑假拔高銜接廣東人民出版社系列答案
津橋教育暑假拔高銜接廣東人民出版社系列答案 波波熊暑假作業江西人民出版社系列答案
波波熊暑假作業江西人民出版社系列答案科目:高中數學 來源: 題型:
【題目】如圖,棱長為![]() 的正方形
的正方形![]() 中,點
中,點![]() ,
,![]() 分別是邊
分別是邊![]() ,
,![]() 上的點,且
上的點,且![]() ,將
,將![]() ,
,![]() 沿
沿![]() ,
,![]() 折起,使得
折起,使得![]() ,
,![]() 兩點重合于
兩點重合于![]() 點上,設
點上,設![]() 與
與![]() 交于
交于![]() 點,過點
點,過點![]() 作
作![]() 于
于![]() 點.
點.
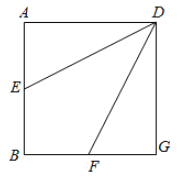
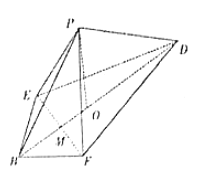
(1)求證:![]() 平面
平面![]() ;
;
(2)求直線![]() 與平面
與平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設橢圓![]() 的左焦點為
的左焦點為![]() ,上頂點為
,上頂點為![]() .已知橢圓的短軸長為4,離心率為
.已知橢圓的短軸長為4,離心率為![]() .
.
(1)求橢圓的方程;
(2)設點![]() 在橢圓上,且異于橢圓的上、下頂點,點
在橢圓上,且異于橢圓的上、下頂點,點![]() 為直線
為直線![]() 與
與![]() 軸的交點,點
軸的交點,點![]() 在
在![]() 軸的負半軸上.若
軸的負半軸上.若![]() (
(![]() 為原點),且
為原點),且![]() ,求證:直線
,求證:直線![]() 的斜率與直線MN的斜率之積為定值.
的斜率與直線MN的斜率之積為定值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,平面ABCD⊥平面CDEF,且四邊形ABCD是梯形,四邊形CDEF是矩形,![]()
![]() ,M是線段DE上的點,滿足DM=2ME.
,M是線段DE上的點,滿足DM=2ME.
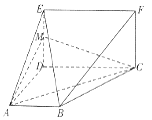
(1)證明:BE//平面MAC;
(2)求直線BF與平面MAC所成角的正弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 的左,右焦點分別為
的左,右焦點分別為![]() ,離心率為
,離心率為![]() ,
,![]() 是
是![]() 上的一個動點.當
上的一個動點.當![]() 是
是![]() 的上頂點時,
的上頂點時,![]() 的面積為
的面積為![]() .
.
(1)求![]() 的方程;
的方程;
(2)設斜率存在的直線![]() 與
與![]() 的另一個交點為
的另一個交點為![]() .若存在點
.若存在點![]() ,使得
,使得![]() ,求
,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知![]() ,
,![]() 是橢圓
是橢圓![]() 的左、右焦點,橢圓
的左、右焦點,橢圓![]() 過點
過點![]() .
.
(1)求橢圓![]() 的方程;
的方程;
(2)過點![]() 的直線
的直線![]() (不過坐標原點)與橢圓
(不過坐標原點)與橢圓![]() 交于
交于![]() ,
,![]() 兩點,且點
兩點,且點![]() 在
在![]() 軸上方,點
軸上方,點![]() 在
在![]() 軸下方,若
軸下方,若![]() ,求直線
,求直線![]() 的斜率.
的斜率.
查看答案和解析>>
科目:高中數學 來源: 題型:
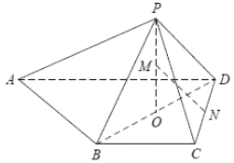
【題目】已知四棱錐![]() ,
,![]() ,
,![]() ,
,![]() ,點
,點![]() 在底面
在底面![]() 上的射影是
上的射影是![]() 的中點
的中點![]() ,
,![]() .
.
(1)求證:直線![]() 平面
平面![]() ;
;
(2)若![]() ,
,![]() 、
、![]() 分別為
分別為![]() 、
、![]() 的中點,求直線
的中點,求直線![]() 與平面
與平面![]() 所成角的正弦值;
所成角的正弦值;
(3)當四棱錐![]() 的體積最大時,求二面角
的體積最大時,求二面角![]() 的大小.
的大小.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】從1到9的九個數字中取三個偶數四個奇數,試問:
(1)能組成多少個沒有重復數字的七位數?
(2)在(1)中的七位數中三個偶數排在一起的有幾個?
(3)在(1)中的七位數中,偶數排在一起、奇數也排在一起的有幾個?
(4)在(1)中任意兩偶然都不相鄰的七位數有幾個?
(答題要求:先列式,后計算 , 結果用具體數字表示.)
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com