
【題目】如圖所示的程序框圖所表示的算法功能是輸出( ) 
A.使1×2×4×6××n≥2017成立的最小整數n
B.使1×2×4×6××n≥2017成立的最大整數n
C.使1×2×4×6××n≥2017成立的最小整數n+2
D.使1×2×4×6××n≥2017成立的最大整數n+2
 世紀百通主體課堂小學課時同步達標系列答案
世紀百通主體課堂小學課時同步達標系列答案 世紀百通優練測系列答案
世紀百通優練測系列答案 百分學生作業本題練王系列答案
百分學生作業本題練王系列答案科目:高中數學 來源: 題型:
【題目】已知各項均為正數的數列{an}的前n項和為Sn , 滿足a ![]() =2Sn+n+4,且a2﹣1,a3 , a7恰為等比數列{bn}的前3項.
=2Sn+n+4,且a2﹣1,a3 , a7恰為等比數列{bn}的前3項.
(1)求數列{an},{bn}的通項公式;
(2)令cn= ![]() ﹣
﹣ ![]() ,求數列{cn}的前n項和Tn .
,求數列{cn}的前n項和Tn .
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設f(x)= ![]() ﹣
﹣ ![]() ,若規定<x>表示不小于x的最小整數,則函數y=<f(x)>的值域是( )
,若規定<x>表示不小于x的最小整數,則函數y=<f(x)>的值域是( )
A.{0,1}
B.{0,﹣1}
C.{﹣1,1}
D.{﹣1,0,1}
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知正方體ABCD﹣A1B1C1D1的棱長為1,給出下列四個命題: ①對角線AC1被平面A1BD和平面B1 CD1三等分;
②正方體的內切球、與各條棱相切的球、外接球的表面積之比為1:2:3;
③以正方體的頂點為頂點的四面體的體積都是 ![]() ;
;
④正方體與以A為球心,1為半徑的球在該正方體內部部分的體積之比為6:π
其中正確命題的序號為 . 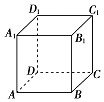
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設實數a∈R,函數 ![]() 是R上的奇函數. (Ⅰ)求實數a的值;
是R上的奇函數. (Ⅰ)求實數a的值;
(Ⅱ)當x∈(1,1)時,求滿足不等式f(1m)+f(1m2)<0的實數m的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知f(x)=ln(1﹣ ![]() )+1,則f(﹣7)+f(﹣5 )+f(﹣3)+f(﹣1)+f(3 )+f( 5)+f(7 )+f( 9)=( )
)+1,則f(﹣7)+f(﹣5 )+f(﹣3)+f(﹣1)+f(3 )+f( 5)+f(7 )+f( 9)=( )
A.0
B.4
C.8
D.16
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com