
【題目】已知圓![]() ,圓
,圓![]() 過點
過點![]() 且與圓
且與圓![]() 相切,設圓心
相切,設圓心![]() 的軌跡為曲線
的軌跡為曲線![]() .
.
(1)求曲線![]() 的方程;
的方程;
(2)點![]() ,
,![]() 為曲線
為曲線![]() 上的兩點(不與點
上的兩點(不與點![]() 重合),記直線
重合),記直線![]() 的斜率分別為
的斜率分別為![]() ,若
,若![]() ,請判斷直線
,請判斷直線![]() 是否過定點. 若過定點,求該定點坐標,若不過定點,請說明理由.
是否過定點. 若過定點,求該定點坐標,若不過定點,請說明理由.
【答案】(1)![]() (2)見解析
(2)見解析
【解析】
(1)結合題意發現圓心C的軌跡是以D,B為焦點的橢圓,建立方程,即可。(2)設出直線PQ的方程,建立方程,將直線方程代入橢圓方程,結合根與系數關系,得到m,k的關系式,計算定點,即可。
(1)設圓C的半徑為r,依題意,|CB|=r,|CD|=4-r,
進而有|CB|+|CD|=4,所以圓心C的軌跡是以D,B為焦點的橢圓,
所以圓心C的軌跡方程為![]() .
.
(2)設點![]() 的坐標分別為
的坐標分別為![]() ,
,
設直線![]() 的方程為
的方程為![]() (直線
(直線![]() 的斜率存在),
的斜率存在),
可得![]() ,
,
整理為:![]() ,
,
聯立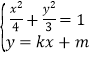 ,消去
,消去![]() 得:
得:![]() ,
,
由![]()
![]() ,有
,有![]() ,
,
有![]() ,
,![]() ,
,
![]() ,可得
,可得![]() ,
,
故有:![]()
![]()
整理得:![]() ,解得:
,解得:![]() 或
或![]()
當![]() 時直線
時直線![]() 的方程為
的方程為![]() ,即
,即![]() ,過定點
,過定點![]() 不合題意,
不合題意,
當![]() 時直線
時直線![]() 的方程為
的方程為![]() ,即
,即![]() ,過定點
,過定點![]() .
.


科目:高中數學 來源: 題型:
【題目】已知橢圓C的中心在原點,焦點在x軸上,離心率等于![]() ,它的一個頂點恰好是拋物線x2=8
,它的一個頂點恰好是拋物線x2=8![]() y的焦點.
y的焦點.
(1)求橢圓C的標準方程;
(2)直線x=﹣2與橢圓交于P,Q兩點,A,B是橢圓上位于直線x=﹣2兩側的動點,若直線AB的斜率為![]() ,求四邊形APBQ面積的最大值.
,求四邊形APBQ面積的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】橢圓![]() 的右焦點為
的右焦點為![]() ,
,![]() 為圓
為圓![]() 與橢圓
與橢圓![]() 的一個公共點,
的一個公共點,![]() .
.
(Ⅰ)求橢圓![]() 的標準方程;
的標準方程;
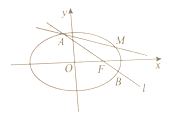
(Ⅱ)如圖,過![]() 作直線
作直線![]() 與橢圓
與橢圓![]() 交于
交于![]() ,
,![]() 兩點,點
兩點,點![]() 為點
為點![]() 關于
關于![]() 軸的對稱點.
軸的對稱點.
(1)求證:![]() ;
;
(2)試問過![]() ,
,![]() 的直線是否過定點?若是,請求出該定點;若不是,請說明理由.
的直線是否過定點?若是,請求出該定點;若不是,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
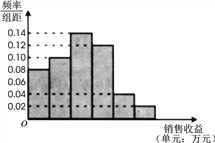
【題目】某公司為了解廣告投入對銷售收益的影響,在若干地區各投入![]() 萬元廣告費用,并將各地的銷售收益繪制成頻率分布直方圖(如圖所示).由于工作人員操作失誤,橫軸的數據丟失,但可以確定橫軸是從
萬元廣告費用,并將各地的銷售收益繪制成頻率分布直方圖(如圖所示).由于工作人員操作失誤,橫軸的數據丟失,但可以確定橫軸是從![]() 開始計數的. [附:回歸直線的斜率和截距的最小二乘估計公式分別為.]
開始計數的. [附:回歸直線的斜率和截距的最小二乘估計公式分別為.]
(1)根據頻率分布直方圖計算圖中各小長方形的寬度;
(2)試估計該公司投入![]() 萬元廣告費用之后,對應銷售收益的平均值(以各組的區間中點值代表該組的取值);
萬元廣告費用之后,對應銷售收益的平均值(以各組的區間中點值代表該組的取值);
(3)該公司按照類似的研究方法,測得另外一些數據,并整理得到下表:
廣告投入 | 1 | 2 | 3 | 4 | 5 |
銷售收益 | 2 | 3 | 2 | 7 |
由表中的數據顯示, ![]() 與
與![]() 之間存在著線性相關關系,請將(2)的結果填入空白欄,并求出
之間存在著線性相關關系,請將(2)的結果填入空白欄,并求出![]() 關于
關于![]() 的回歸直線方程.
的回歸直線方程.

查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設函數![]() ,則下列命題中正確的個數是( )
,則下列命題中正確的個數是( )
①當![]() 時,函數
時,函數![]() 在
在![]() 上有最小值;②當
上有最小值;②當![]() 時,函數
時,函數![]() 在
在![]() 是單調增函數;③若
是單調增函數;③若![]() ,則
,則![]() ;④方程
;④方程![]() 可能有三個實數根.
可能有三個實數根.
A.1B.2C.3D.4
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知數集![]() (
(![]() ,
,![]() )具有性質
)具有性質![]() :對任意
:對任意![]() 、
、![]() (
(![]() ),
),![]() 與
與![]() 兩數中至少有一個屬于集合
兩數中至少有一個屬于集合![]() ,現給出以下四個命題:①數集
,現給出以下四個命題:①數集![]() 具有性質
具有性質![]() ;②數集
;②數集![]() 具有性質
具有性質![]() ;③若數集
;③若數集![]() 具有性質
具有性質![]() ,則
,則![]() ;④若數集
;④若數集![]() (
(![]() )具有性質
)具有性質![]() ,則
,則![]() ;其中真命題有________(填寫序號)
;其中真命題有________(填寫序號)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,四邊形ABCD中,AD∥BC,AD=AB,∠BCD=45°,∠BAD=90°,將△ABD沿BD折起,使平面ABD⊥平面BCD,構成四面體ABCD,則在四面體ABCD中,下列結論正確的是( )

A. 平面ABD⊥平面ABC B. 平面ADC⊥平面BDC
C. 平面ABC⊥平面BDC D. 平面ADC⊥平面ABC
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某城市上年度電價為0.80元/千瓦時,年用電量為![]() 千瓦時.本年度計劃將電價降到0.55元/千瓦時~0.7元/千瓦時之間,而居民用戶期望電價為0.40元/千瓦時(該市電力成本價為0.30元/千瓦時),經測算,下調電價后,該城市新增用電量與實際電價和用戶期望電價之差成反比,比例系數為
千瓦時.本年度計劃將電價降到0.55元/千瓦時~0.7元/千瓦時之間,而居民用戶期望電價為0.40元/千瓦時(該市電力成本價為0.30元/千瓦時),經測算,下調電價后,該城市新增用電量與實際電價和用戶期望電價之差成反比,比例系數為![]() .試問當地電價最低為多少元/千瓦時,可保證電力部門的收益比上年度至少增加20%.
.試問當地電價最低為多少元/千瓦時,可保證電力部門的收益比上年度至少增加20%.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】太極圖是由黑白兩個魚形紋組成的圖案,太極圖展現了一種相互轉化,相互統一的和諧美.定義:能夠將圓![]() 的周長和面積同時等分成兩部分的函數稱為圓
的周長和面積同時等分成兩部分的函數稱為圓![]() 的一個“太極函數”.下列有關說法中正確的個數是( )個
的一個“太極函數”.下列有關說法中正確的個數是( )個

①對圓![]() 的所有非常數函數的太極函數中,一定不能為偶函數;
的所有非常數函數的太極函數中,一定不能為偶函數;
②函數![]() 是圓
是圓![]() 的一個太極函數;
的一個太極函數;
③存在圓![]() ,使得
,使得![]() 是圓
是圓![]() 的太極函數;
的太極函數;
④直線![]() 所對應的函數一定是圓
所對應的函數一定是圓![]() 的太極函數.
的太極函數.
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com