
【題目】已知f(x)=2x2﹣3x+1,g(x)=ksin(x﹣ ![]() )(k≠0).
)(k≠0).
(1)設f(x)的定義域為[0,3],值域為A; g(x)的定義域為[0,3],值域為B,且AB,求實數k的取值范圍.
(2)若方程f(sinx)+sinx﹣a=0在[0,2π)上恰有兩個解,求實數a的取值范圍.
【答案】
(1)解:當x∈[0,3]時,由于f(x)=2x2﹣3x+1圖象的對稱軸為 ![]() ,且開口向上,
,且開口向上,
可知 ![]() ,f(x)max=f(3)=10,
,f(x)max=f(3)=10,
所以f(x)的值域 ![]() ;
;
當x∈[0,3]時, ![]() ,
, ![]() ;所以當k>0時,g(x)的值域
;所以當k>0時,g(x)的值域 ![]() ;
;
所以當k<0時,g(x)的值域 ![]() ;
;
又∵AB,所以 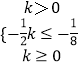 或
或 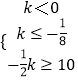 ;
;
即 k≥10或k≤﹣20;
(2)解:∵f(sinx)+sinx﹣a=0,所以2sin2x﹣2sinx+1﹣a=0在x∈[0,2π)上恰有兩個解,…
設t=sinx,則t∈[﹣1,1],令h(t)=2t2﹣2t+1﹣a,
①當t∈(﹣1,1)時,由題意h(t)=0恰有一個解或者有兩個相等的解,
即h(﹣1)h(﹣1)<0或△=4﹣8(1﹣a)=0,即1<a<5或 ![]()
②若t=﹣1是方程2t2﹣2t+1﹣a=0的一個根,此時a=5,且方程的另一個根為t=2,于是sinx=﹣1或sinx=2,
因此 ![]() ,不符合題意,故a=5(舍);
,不符合題意,故a=5(舍);
③若t=1是方程2t2﹣2t+1﹣a=0的一個根,此時a=1,且方程的另一個根為t=0,于是sinx=1或sinx=0,
因此x=0或 ![]() 或π,不符合題意,故a=1(舍);
或π,不符合題意,故a=1(舍);
綜上,a的取值范圍是1<a<5或 ![]() .
.
【解析】(1)根據二次函數和正弦函數的圖象與性質,分別求出f(x)、g(x)在區間[0,3]上的最值即得值域A、B;再根據AB求出k的取值范圍;(2)根據f(sinx)+sinx﹣a=0在x∈[0,2π)上恰有兩個解,利用換元法設t=sinx,t∈[﹣1,1],構造函數h(t)=2t2﹣2t+1﹣a,討論t的取值范圍,從而求出實數a的取值范圍.
【考點精析】解答此題的關鍵在于理解二次函數的性質的相關知識,掌握當![]() 時,拋物線開口向上,函數在
時,拋物線開口向上,函數在![]() 上遞減,在
上遞減,在![]() 上遞增;當
上遞增;當![]() 時,拋物線開口向下,函數在
時,拋物線開口向下,函數在![]() 上遞增,在
上遞增,在![]() 上遞減.
上遞減.


 階梯計算系列答案
階梯計算系列答案科目:高中數學 來源: 題型:
【題目】自選題:已知曲線C1: ![]() (θ為參數),曲線C2:
(θ為參數),曲線C2: 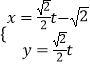 (t為參數).
(t為參數).
(1)指出C1 , C2各是什么曲線,并說明C1與C2公共點的個數;
(2)若把C1 , C2上各點的縱坐標都壓縮為原來的一半,分別得到曲線C1′,C2′.寫出C1′,C2′的參數方程.C1′與C2′公共點的個數和C與C2公共點的個數是否相同?說明你的理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知關于![]() 的二次函數
的二次函數![]() .
.
(1)設集合![]() 和
和![]() ,分別從集合
,分別從集合![]() 中隨機取一個數作為
中隨機取一個數作為![]() 和
和![]() ,求函數
,求函數![]() 在區間
在區間![]() 上是增函數的概率;
上是增函數的概率;
(2)設點![]() 是區域
是區域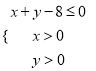 內的隨機點, 求函數
內的隨機點, 求函數![]() 在區間
在區間![]() 上是增函數的概率.
上是增函數的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某種產品每件成本為6元,每件售價為![]() 元(
元(![]() ),年銷售
),年銷售![]() 萬件,若已知
萬件,若已知![]() 與
與![]() 成正比,且售價為10元時,年銷量為28萬件.
成正比,且售價為10元時,年銷量為28萬件.
(1)求年銷售利潤![]() 關于售價
關于售價![]() 的函數關系式.
的函數關系式.
(2)求售價為多少時,年利潤最大,并求出最大年利潤.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某種產品的質量以其質量指標值衡量,并依據質量指標值劃分等級如下表:
質量指標值 |
|
|
|
等級 | 三等品 | 二等品 | 一等品 |
從某企業生產的這種產品中抽取200件,檢測后得到如下的頻率分布直方圖:
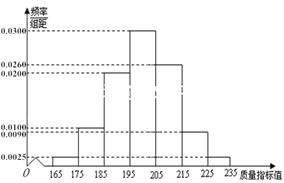
(Ⅰ)根據以上抽樣調查數據,能否認為該企業生產的這種產品符合“一、二等品至少要占全部產品92%”的規定?
(Ⅱ)在樣本中,按產品等級用分層抽樣的方法抽取8件,再從這8件產品中隨機抽取4件,求抽取的4件產品中,一、二、三等品都有的概率;
(Ⅲ)該企業為提高產品質量,開展了“質量提升月”活動,活動后再抽樣檢測,產品質量指標值![]() 近似滿足
近似滿足![]() ,則“質量提升月”活動后的質量指標值的均值比活動前大約提升了多少?
,則“質量提升月”活動后的質量指標值的均值比活動前大約提升了多少?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】汽車廠生產![]() 三類轎車,每類轎車均有舒適型和標準型兩種型號,某月的產量如下表(單位:輛):按類用分層抽樣的方法在這個月生產的轎車中抽取50輛,其中有A類轎車10輛.
三類轎車,每類轎車均有舒適型和標準型兩種型號,某月的產量如下表(單位:輛):按類用分層抽樣的方法在這個月生產的轎車中抽取50輛,其中有A類轎車10輛.
轎車 | 轎車 | 轎車 | |
舒適型 | 100 | 150 |
|
標準型 | 300 | 450 | 600 |
(1)求![]() 的值;
的值;
(2)用分層抽樣的方法在![]() 類轎車中抽取一個容量為5的樣本.將該樣本看成一個總體,從中任取
類轎車中抽取一個容量為5的樣本.將該樣本看成一個總體,從中任取
2輛,求至少有1輛舒適型轎車的概率;
(3)用隨機抽樣的方法從![]() 類舒適型轎車中抽取8輛,經檢測它們的得分如下:
類舒適型轎車中抽取8輛,經檢測它們的得分如下:![]() . 把這8輛轎車的得分看成一個總體,從中任取一個數,求該數與樣本平均數之差的絕對 值不超過
. 把這8輛轎車的得分看成一個總體,從中任取一個數,求該數與樣本平均數之差的絕對 值不超過![]() 的概率.
的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】假設要抽查某企業生產的某種品牌的袋裝牛奶的質量是否達標,現從700袋牛奶中抽取50袋進行檢驗,利用隨機數表抽取樣本時,先將700袋牛奶按001,002,…,700進行編號,如果從隨機數表第3行第1組開始向右讀,最先讀到的5袋牛奶的編號是614,593,379,242,203,請你以此方式繼續向右讀數,隨后讀出的3袋牛奶的編號是________.(下列摘取了隨機數表第1行至第5行)

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com