Question

【題目】已知橢圓C： =1（a＞b＞0）的長軸長為6，且橢圓C與圓M：（x﹣2）2+y2= 的公共弦長為 ．
（1）求橢圓C的方程，
（2）過點P（0，2）作斜率為k（k≠0）的直線l與橢圓C交于兩點A，B，試判斷在x軸上是否存在點D，使得△ADB為以AB為底邊的等腰三角形，若存在，求出點D的橫坐標的取值范圍，若不存在，請說明理由．

Answer 1

【答案】
（1）

解：由題意可知：2a=6，則a=3，圓M：（x﹣2）2+y2= ，圓心（2，0），半徑為 ，

由題意可知：橢圓經過點（2， ），代入橢圓方程： ，解得：b2=8，

∴橢圓的標準方程：

（2）

解：由題意可知直線l：y=kx+2，A（x1，y1），B（x2，y2），

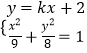，整理得：（9k2+8）x2+36kx﹣36=0，

x1+x2=﹣ ，x1x2= ，

假設存在點D（m，0）滿足題意，

取AB中點M（x0，y0）則MB⊥AB，

由x0= =﹣ ，則y0=kx0+2= ，

則M（﹣ ， ），

由題意可知：kkMD=﹣ =﹣1，

整理得：9k2m+2k+2m=0，

∴m= =﹣ ≥﹣ ，

存在點D，且D點橫坐標取值范圍[﹣ ，+∞）

【解析】（1）由2a=6，則a=3，由圓的方程，可得橢圓過點（2， ），代入橢圓方程，即可求得b的值，求得橢圓方程；（2）設直線l的方程，代入橢圓方程，利用韋達定理及中點坐標公式，求得AB的中點M點坐標，kkMD=﹣1，即可求得m的表達式，利用基本不等式的性質，即可求得點D的橫坐標的取值范圍．