
【題目】已知向量 ![]() ,向量
,向量 ![]() ,函數f(x)=
,函數f(x)= ![]() .
.
(1)求函數f(x)的單調遞增區間;
(2)將函數y=f(x)的圖象上所有點向右平行移動 ![]() 個單位長度,得函數y=g(x)的圖象,求函數y=g(x)在區間[0,π]上的值域.
個單位長度,得函數y=g(x)的圖象,求函數y=g(x)在區間[0,π]上的值域.
【答案】
(1)解:∵向量 ![]() ,向量
,向量 ![]() ,
,
∴函數f(x)= ![]() =
= ![]() sinx﹣cosx=2sin(x﹣
sinx﹣cosx=2sin(x﹣ ![]() ),
),
令2kπ﹣ ![]() ≤x﹣
≤x﹣ ![]() ≤2kπ+
≤2kπ+ ![]() ,求得2kπ﹣
,求得2kπ﹣ ![]() ≤x≤2kπ+
≤x≤2kπ+ ![]() ,
,
可得函數的增區間為[2kπ﹣ ![]() ,2kπ+
,2kπ+ ![]() ],k∈Z
],k∈Z
(2)解:將函數y=f(x)的圖象上所有點向右平行移動 ![]() 個單位長度,
個單位長度,
得函數y=g(x)=2sin(x﹣ ![]() ﹣
﹣ ![]() )=2sin(x﹣
)=2sin(x﹣ ![]() ) 的圖象,
) 的圖象,
∵x∈[0,π],∴x﹣ ![]() ∈[﹣
∈[﹣ ![]() ,
, ![]() ],
],
∴sin(x﹣ ![]() )∈[﹣
)∈[﹣ ![]() ,1],∴g(x)∈[
,1],∴g(x)∈[ ![]() ,2],
,2],
即函數y=g(x)在區間[0,π]上的值域為[ ![]() ,2]
,2]
【解析】(1)利用兩個向量的數量積的運算法則求得f(x)的解析式,再利用正弦函數的單調性,求得函數f(x)的單調遞增區間.(2)由條件利用函數y=Asin(ωx+φ)的圖象變換規律求得g(x)的解析式,再利用正弦函數的定義域和值域,求得函數y=g(x)在區間[0,π]上的值域.
【考點精析】根據題目的已知條件,利用函數y=Asin(ωx+φ)的圖象變換的相關知識可以得到問題的答案,需要掌握圖象上所有點向左(右)平移![]() 個單位長度,得到函數
個單位長度,得到函數![]() 的圖象;再將函數
的圖象;再將函數![]() 的圖象上所有點的橫坐標伸長(縮短)到原來的
的圖象上所有點的橫坐標伸長(縮短)到原來的![]() 倍(縱坐標不變),得到函數
倍(縱坐標不變),得到函數![]() 的圖象;再將函數
的圖象;再將函數![]() 的圖象上所有點的縱坐標伸長(縮短)到原來的
的圖象上所有點的縱坐標伸長(縮短)到原來的![]() 倍(橫坐標不變),得到函數
倍(橫坐標不變),得到函數![]() 的圖象.
的圖象.


 學期復習一本通學習總動員期末加暑假延邊人民出版社系列答案
學期復習一本通學習總動員期末加暑假延邊人民出版社系列答案 芒果教輔暑假天地重慶出版社系列答案
芒果教輔暑假天地重慶出版社系列答案科目:高中數學 來源: 題型:
【題目】某公園有一個直角三角形地塊,現計劃把它改造成一塊矩形和兩塊三角形區域.如圖,矩形區域用于娛樂城設施的建設,三角形BCD區域用于種植甲種觀賞花卉,三角形CAE區域用于種植乙種觀賞花卉.已知OA=4千米,OB=3千米,∠AOB=90°,甲種花卉每平方千米造價1萬元,乙種花卉每平方千米造價4萬元,設OE=x千米.試建立種植花卉的總造價為y(單位:萬元)關于x的函數關系式;求x為何值時,種植花卉的總造價最小,并求出總造價. 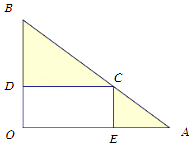
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】股票市場的前身是起源于1602年荷蘭人在阿姆斯特河大橋上進行荷屬東印度公司股票的買賣,而正規的股票市場最早出現在美國.2017年2月26號,中國證監會主席劉士余談了對股市的幾點建議,給廣大股民樹立了信心.最近,張師傅和李師傅要將家中閑置資金進行投資理財.現有兩種投資方案,且一年后投資盈虧的情況如下:
(1)投資股市:
投資結果 | 獲利 | 不賠不賺 | 虧損 |
概率 |
|
|
|
(2)購買基金:
投資結果 | 獲利 | 不賠不賺 | 虧損 |
概率 |
|
|
|
(Ⅰ)當![]() 時,求
時,求![]() 的值;
的值;
(Ⅱ)已知“購買基金”虧損的概率比“投資股市”虧損的概率小,求![]() 的取值范圍;
的取值范圍;
(Ⅲ)已知張師傅和李師傅兩人都選擇了“購買基金”來進行投資,假設三種投資結果出現的可能性相同,求一年后他們兩人中至少有一人獲利的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在三棱柱ABC﹣A1B1C1中,側面ABB1A1 , ACC1A1均為正方形,AB=AC=1,∠BAC=90,點D是棱B1C1的中點. 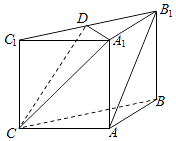
(1)求證:AB1∥平面A1DC;
(2)求證:A1D⊥平面BB1C1C.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知Sn是等差數列{an}的前n項和,且S8>S9>S7 , 給出下列四個命題:
①d<0;
②S16<0;
③數列{Sn}中的最大項為S15;
④|a8|>|a9|.
其中正確命題有 .
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 過點
過點 ,順次連接橢圓的四個頂點得到的四邊形的面積為
,順次連接橢圓的四個頂點得到的四邊形的面積為![]() ,點
,點![]() .
.
(Ⅰ)求橢圓![]() 的方程.
的方程.
(Ⅱ)已知點![]() ,是橢圓
,是橢圓![]() 上的兩點.
上的兩點.
(ⅰ)若![]() ,且
,且![]() 為等邊三角形,求
為等邊三角形,求![]() 的面積;
的面積;
(ⅱ)若![]() ,證明:
,證明: ![]() 不可能為等邊三角形.
不可能為等邊三角形.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知![]() ,且
,且![]() ,設命題p:函數
,設命題p:函數![]() 在
在![]() 上單調遞減;命題q:函數
上單調遞減;命題q:函數![]() 在
在![]() 上為增函數,
上為增函數,
(1)若“p且q”為真,求實數c的取值范圍
(2)若“p且q”為假,“p或q”為真,求實數c的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com