【題目】以下統計表和分布圖取自《清華大學2019年畢業生就業質量報告》.
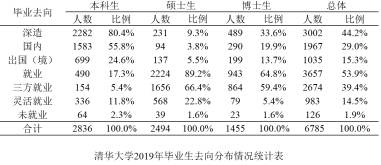
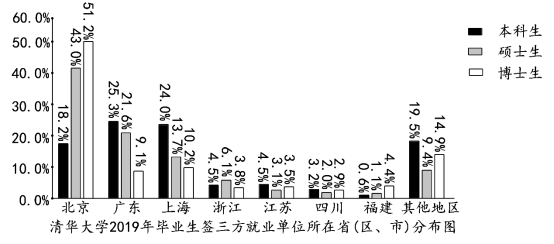
則下列選項錯誤的是（ ）
A.清華大學2019年畢業生中，大多數本科生選擇繼續深造，大多數碩士生選擇就業
B.清華大學2019年畢業生中，碩士生的就業率比本科生高
C.清華大學2019年簽三方就業的畢業生中，本科生的就業城市比碩士生的就業城市分散
D.清華大學2019年簽三方就業的畢業生中，留北京人數超過一半
【答案】D
【解析】
根據統計表和分布圖中的數據信息，對選項進行逐一分析判斷，得出答案.
A. 根據統計表，本科生選擇繼續深造的比例為80.4%，碩士生選擇就業的比例為89.2%，所以判斷正確.
B. 根據統計表，本科生就業率17.3%, 碩士生的就業率為為89.2%.判斷正確.
C. 根據分布圖，簽三方就業的畢業生中，碩士生的就業城市主要分布在北京、廣東、上海；本科生的就業城市相對比較分散.判斷正確.
D. 根據分布圖, 畢業學生中，本科生人數占絕大多數，簽三方就業的畢業生中,留在北京的本科生占18.2%，而碩士生和博士生分別占43.0%、51.2%，
所以畢業生留在北京的沒有達到一半，所以判斷錯誤.
故選：D
核心素養學練評系列答案
單元期中期末卷系列答案科目：高中數學 來源： 題型：
【題目】正態分布有極其廣泛的實際背景，生產與科學實驗中很多隨機變量的概率分布都可以近似地用正態分布來描述.例如，同一種生物體的身長、體重等指標.隨著“綠水青山就是金山銀山”的觀念不斷的深入人心，環保工作快速推進，很多地方的環境出現了可喜的變化.為了調查某水庫的環境保護情況，在水庫中隨機捕撈了100條魚稱重.經整理分析后發現，魚的重量x（單位：kg）近似服從正態分布
，如圖所示，已知
.
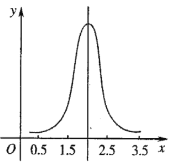
（Ⅰ）若從水庫中隨機捕撈一條魚，求魚的重量在
內的概率；
（Ⅱ）（ⅰ）從捕撈的100條魚中隨機挑出6條魚測量體重，6條魚的重量情況如表.
重量范圍（單位：kg） |
|
|
|
條數 | 1 | 3 | 2 |
為了進一步了解魚的生理指標情況，從6條魚中隨機選出3條，記隨機選出的3條魚中體重在
內的條數為X，求隨機變量X的分布列和數學期望；
（ⅱ）若將選剩下的94條魚稱重做標記后立即放生.兩周后又隨機捕撈1000條魚，發現其中帶有標記的有2條.為了調整生態結構，促進種群的優化，預備捕撈體重在
內的魚的總數的40%進行出售，試估算水庫中魚的條數以及應捕撈體重在內的魚的條數.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知橢圓C：
+
=1（a＞b＞0）的離心率為
，直線l：x+2y=4與橢圓有且只有一個交點T．
（I）求橢圓C的方程和點T的坐標；
（Ⅱ）O為坐標原點，與OT平行的直線l′與橢圓C交于不同的兩點A，B，直線l′與直線l交于點P，試判斷
是否為定值，若是請求出定值，若不是請說明理由．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某地區經過一年的新農村建設，農村的經濟收入增加了一倍．實現翻番．為更好地了解該地區農村的經濟收入變化情況，統計了該地區新農村建設前后農村的經濟收入構成比例．得到如下餅圖：
則下面結論中不正確的是
A. 新農村建設后，種植收入減少
B. 新農村建設后，其他收入增加了一倍以上
C. 新農村建設后，養殖收入增加了一倍
D. 新農村建設后，養殖收入與第三產業收入的總和超過了經濟收入的一半
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】2012年12月18日，作為全國首批開展空氣質量新標準監測的74個城市之一，鄭州市正式發布
數據.資料表明，近幾年來，鄭州市霧霾治理取得了很大成效，空氣質量與前幾年相比得到了很大改善.鄭州市設有9個監測站點監測空氣質量指數（
），其中在輕度污染區、中度污染區、重度污染區分別設有2,5,2個監測站點，以9個站點測得的的平均值為依據，播報我市的空氣質量.
（Ⅰ）若某日播報的為118，已知輕度污染區的平均值為74，中度污染區的平均值為114，求重度污染區的平均值；
（Ⅱ）如圖是2018年11月的30天中的分布，11月份僅有一天在
內.
組數 | 分組 | 天數 |
第一組 |
| 3 |
第二組 |
| 4 |
第三組 |
| 4 |
第四組 |
| 6 |
第五組 |
| 5 |
第六組 |
| 4 |
第七組 |
| 3 |
第八組 |
| 1 |
①鄭州市某中學利用每周日的時間進行社會實踐活動，以公布的為標準，如果小于180，則去進行社會實踐活動.以統計數據中的頻率為概率，求該校周日進行社會實踐活動的概率；
②在“創建文明城市”活動中，驗收小組把鄭州市的空氣質量作為一個評價指標，從當月的空氣質量監測數據中抽取3天的數據進行評價，設抽取到不小于180的天數為
，求的分布列及數學期望.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】為了更好地貫徹黨的“五育并舉”的教育方針，某市要對全市中小學生“體能達標”情況進行了解，決定通過隨機抽樣選擇幾個樣本校對學生進行體能達標測試，并規定測試成績低于60分為不合格，否則為合格，若樣本校學生不合格人數不超過其總人數的5%，則該樣本校體能達標為合格.已知某樣本校共有1000名學生，現從中隨機抽取40名學生參加體能達標測試，首先將這40名學生隨機分為甲、乙兩組，其中甲乙兩組學生人數的比為3:2，測試后，兩組各自的成績統計如下：甲組的平均成績為70，方差為16，乙組的平均成績為80，方差為36.
（1）估計該樣本校學生體能測試的平均成績；
（2）求該樣本校40名學生測試成績的標準差s；
（3）假設該樣本校體能達標測試成績服從正態分布
，用樣本平均數
作為
的估計值
，用樣本標準差s作為
的估計值
，利用估計值估計該樣本校學生體能達標測試是否合格？
（注：1.本題所有數據的最后結果都精確到整數；2若隨機變量z服從正態分布，則
，
，
）
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】在多面體
中，正方形
和矩形
互相垂直，
，
分別是
和
的中點，
.
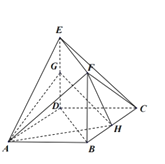
（Ⅰ）求證：
平面.
（Ⅱ）在邊所在的直線上存在一點
，使得
平面
，求
的長；
（Ⅲ）求直線
與平面
所成角的正弦值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
