
【題目】己知函數![]() ,
, ![]() .
.
(I)求函數![]() 的單調區間;
的單調區間;
(II)設![]() ,已知函數
,已知函數![]() 在
在![]() 上是增函數.
上是增函數.
(1)研究函數![]() 上零點的個數;
上零點的個數;
(ii)求實數c的取值范圍.
【答案】(Ⅰ)詳見解析; (Ⅱ)(1)1個;(2) ![]() .
.
【解析】試題分析(1) 對函數求導,①當![]() 時,
時, ![]() 在
在![]() 上是減函數,在
上是減函數,在![]() 上是增函數;②當
上是增函數;②當![]() 時,
時, ![]() 在
在![]() 上是增函數,在
上是增函數,在![]() 上是減函數;(2) (1)當
上是減函數;(2) (1)當![]() 時,函數
時,函數![]()
![]() ,
, ![]() ,
, ![]() 在
在![]() 上單調遞減.又
上單調遞減.又![]() ,
, ![]() ,由函數的零點存在性定理及其單調性知,
,由函數的零點存在性定理及其單調性知, ![]() 在
在![]() 上零點的個數為1.(2)由(1)知,當
上零點的個數為1.(2)由(1)知,當![]() 時,
時, ![]() >0,當
>0,當![]() 時,
時, ![]() <0.∴當
<0.∴當![]() 時,
時, ![]() =
=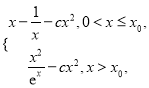 求導,得
求導,得![]() 在
在![]() ,
, ![]() 上恒成立. ①當
上恒成立. ①當![]() 時,
時, ![]() min=
min= ![]() 極小值=
極小值= ![]()
![]() ,故“
,故“![]() 在
在![]() 上恒成立”,只需
上恒成立”,只需![]()
![]() .②當
.②當![]() 時,當
時,當![]() 時,
時, ![]() 在
在![]() 上恒成立,綜合①②知,
上恒成立,綜合①②知, ![]() 的取值范圍是
的取值范圍是![]() .
.
試題解析:(Ⅰ)∵![]() ,
,
∴![]() ,
,
①當![]() 時,
時,
在![]() 時,
時, ![]() ,
,
在![]() 時,
時, ![]() ,
,
故![]() 在
在![]() 上是減函數,在
上是減函數,在![]() 上是增函數;
上是增函數;
②當![]() 時,
時,
在![]() 時,
時, ![]() ,
,
在![]() 時,
時, ![]() ,
,
故![]() 在
在![]() 上是增函數,在
上是增函數,在![]() 上是減函數;
上是減函數;
(Ⅱ)(1)當![]() 時,函數
時,函數![]()
![]() ,
,
求導,得![]() ,
,
當![]() 時,
時, ![]() 恒成立,
恒成立,
當![]() 時,
時, 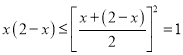 ,
,
∴![]()
![]() ,
,
∴![]() 在
在![]() 上恒成立,故
上恒成立,故![]() 在
在![]() 上單調遞減.
上單調遞減.
又![]() ,
, ![]() ,
,
曲線![]() 在[1,2]上連續不間斷,
在[1,2]上連續不間斷,
∴由函數的零點存在性定理及其單調性知,唯一的![]() ∈(1,2),使
∈(1,2),使![]() ,
,
所以,函數![]() 在
在![]() 上零點的個數為1.
上零點的個數為1.
(2)由(1)知,當![]() 時,
時, ![]() >0,當
>0,當![]() 時,
時, ![]() <0.
<0.
∴當![]() 時,
時, ![]() =
=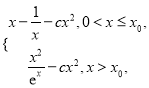
求導,得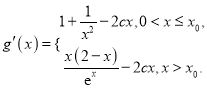
由函數![]() 在
在![]() 上是增函數,且曲線
上是增函數,且曲線![]() 在
在![]() 上連續不斷知:
上連續不斷知:
![]() 在
在![]() ,
, ![]() 上恒成立.
上恒成立.
①當![]() 時,
時, ![]()
![]() 上恒成立,
上恒成立,
即![]() 在
在![]() 上恒成立,
上恒成立,
記![]() ,
, ![]() ,則
,則![]() ,
, ![]() ,
,
當 ![]() 變化時,
變化時, ![]() ,
, ![]() 變化情況列表如下:
變化情況列表如下:
|
| 3 |
|
|
| 0 |
|
|
| 極小值 |
|
∴![]() min=
min= ![]() 極小值=
極小值= ![]()
![]() ,
,
故“![]() 在
在![]() 上恒成立”,只需
上恒成立”,只需![]()
![]() ,即
,即![]() .
.
②當![]() 時,
時, ![]()
![]() ,
,
當![]() 時,
時, ![]() 在
在![]() 上恒成立,
上恒成立,
綜合①②知,當![]() 時,函數
時,函數![]() 在
在![]() 上是增函數.
上是增函數.
故實數![]() 的取值范圍是
的取值范圍是![]() .
.


 每日10分鐘口算心算速算天天練系列答案
每日10分鐘口算心算速算天天練系列答案科目:高中數學 來源: 題型:
【題目】如圖是某社區工會對當地企業工人月收入情況進行一次抽樣調查后畫出的頻率分布直方圖,其中第二組月收入在[1.5,2)千元的頻數為300,則此次抽樣的樣本容量為( ) 
A.1000
B.2000
C.3000
D.4000
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在四棱錐P﹣ABCED中,PD⊥面ABCD,四邊形ABCD為平行四邊形,∠DAB=60°,AB=PA=2AD=4, 
(1)若E為PC中點,求證:PA∥平面BDE
(2)求三棱錐D﹣BCP的體積.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() :
: ![]() 過點
過點![]() ,
, ![]() 為橢圓的半焦距,且
為橢圓的半焦距,且![]() ,過點
,過點![]() 作兩條互相垂直的直線
作兩條互相垂直的直線![]() ,
, ![]() 與橢圓
與橢圓![]() 分別交于另兩點
分別交于另兩點![]() ,
, ![]() .
.
(1)求橢圓![]() 的方程;
的方程;
(2)若直線![]() 的斜率為
的斜率為![]() ,求
,求![]() 的面積;
的面積;
(3)若線段![]() 的中點在
的中點在![]() 軸上,求直線
軸上,求直線![]() 的方程.
的方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() 在
在![]() 上是減函數,在
上是減函數,在![]() 上是增函數,函數
上是增函數,函數![]() 在
在![]() 上有三個零點.
上有三個零點.
(1)求![]() 的值;
的值;
(2)若1是其中一個零點,求![]() 的取值范圍;
的取值范圍;
(3)若![]() ,試問過點(2,5)可作多少條直線與曲線y=g(x)相切?請說明理由.
,試問過點(2,5)可作多少條直線與曲線y=g(x)相切?請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
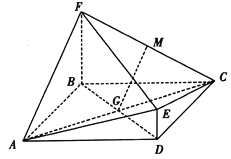
【題目】如圖,菱![]() 與四邊形BDEF相交于BD,
與四邊形BDEF相交于BD, ![]() 平面ABCD,DE//BF,BF=2DE,AF⊥FC,M為CF的中點,
平面ABCD,DE//BF,BF=2DE,AF⊥FC,M為CF的中點, ![]() .
.
(I)求證:GM//平面CDE;
(II)求證:平面ACE⊥平面ACF.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】己知函數![]() (其中e為自然對數的底數),
(其中e為自然對數的底數), ![]() .
.
(I)求函數![]() 的單調區間;
的單調區間;
(II)設![]() ,.已知直線
,.已知直線![]() 是曲線
是曲線![]() 的切線,且函數
的切線,且函數![]() 上是增函數.
上是增函數.
(i)求實數![]() 的值;
的值;
(ii)求實數c的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設p:實數x滿足x2﹣4ax+3a2<0,其中a>0,命題q:實數x滿足 ![]() .
.
(1)若a=1,且p∨q為真,求實數x的取值范圍;
(2)若p是q的必要不充分要條件,求實數a的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知等差數列{an}滿足:a3=3,a5+a7=12,{an}的前n項和為Sn .
(1)求an及Sn;
(2)令bn= ![]() (n∈N*),求數列{bn}的前n項和Tn .
(n∈N*),求數列{bn}的前n項和Tn .
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com