【題目】甲、乙兩名籃球運動員，甲投籃一次命中的概率為
，乙投籃一次命中的概率為
，若甲、乙各投籃三次，設
為甲、乙投籃命中的次數的差的絕對值，其中甲、乙兩人投籃是否命中相互沒有影響.
（1）若甲、乙第一次投籃都命中，求甲獲勝（甲投籃命中數比乙多）的概率；
（2）求的分布列及數學期望.
優翼小幫手同步口算系列答案科目：高中數學 來源： 題型：
【題目】一個生產公司投資A生產線500萬元，每萬元可創造利潤
萬元，該公司通過引進先進技術，在生產線A投資減少了x萬元，且每萬元的利潤提高了
；若將少用的x萬元全部投入B生產線，每萬元創造的利潤為
萬元，其中
．
若技術改進后A生產線的利潤不低于原來A生產線的利潤，求x的取值范圍；
若生產線B的利潤始終不高于技術改進后生產線A的利潤，求a的最大值．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知定義在[e，+∞）上的函數f（x）滿足f（x）+xlnxf′（x）＜0且f（2018）＝0，其中f′（x）是函數
的導函數，e是自然對數的底數，則不等式f（x）＞0的解集為（ ）
A. [e，2018） B. [2018，+∞） C. （e，+∞） D. [e，e+1）
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖，四棱錐
，
平面
，且
，底面為直角梯形，
，
，
，
，，，
、
分別為
、
的中點，平面
與
的交點為
.
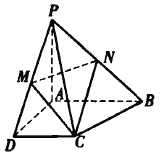
（1）求
的長度；
（2）求截面的底面所成二面角的大小；
（3）求點
到平面的距離.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】（2015秋運城期中）已知函數f（x）=（log2x﹣2）（log4x﹣
）．
（1）當x∈[1，4]時，求該函數的值域；
（2）若f（x）≤mlog2x對于x∈[4，16]恒成立，求m得取值范圍．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】[選修4-4：坐標系與參數方程]
在直角坐標系
中，曲線
的參數方程為
（
為參數），以原點
為極點，
軸的正半軸為極軸建立極坐標系，曲線
的極坐標方程為
．
（1）寫出曲線的普通方程和曲線的直角坐標方程；
（2）已知點
是曲線上的動點，求點到曲線的最小距離．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
