Question

如圖，直三棱柱ABC-A₁B₁C₁中，AC⊥AB，AB=2AA₁，M是AB的中點，△A₁MC₁是等腰三角形，D為CC₁的中點，E為BC上一點．
（1）若DE∥平面A₁MC₁，求

CE

EB

；
（2）平面A₁MC₁將三棱柱ABC-A₁B₁C₁分成兩個部分，求較小部分與較大部分的體積之比．

Answer 1

考點：棱柱、棱錐、棱臺的體積,直線與平面平行的判定

專題：綜合題,空間位置關系與距離

分析：（1）先證明A₁，M，N，C₁四點共面，利用DE∥平面A₁MC₁，可得DE∥C₁N，利用D為CC₁的中點，即可求

CE

EB

；
（2）將幾何體AA₁M-CC₁N補成三棱柱AA₁M-CC₁F，求出幾何體AA₁M-CC₁N的體積、直三棱柱ABC-A₁B₁C₁體積，即可求較小部分與較大部分的體積之比．

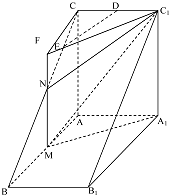
解答： 解：（1）取BC中點為N，連結MN，C₁N，…（1分）
∵M，N分別為AB，CB中點
∴MN∥AC∥A₁C₁，
∴A₁，M，N，C₁四點共面，…（3分）
且平面BCC₁B₁∩平面A₁MNC₁=C₁N
又DE?平面BCC₁B₁，且DE∥平面A₁MC₁
∴DE∥C₁N
∵D為CC₁的中點，
∴E是CN的中點，…（5分）
∴

CE

EB

=

1

3

．                                                 …（6分）
（2）∵三棱柱ABC-A₁B₁C₁為直三棱柱，∴AA₁⊥平面ABC，
又AC⊥AB，則AC⊥平面ABB₁A₁
設AB=2AA₁=2，又三角形A₁MC₁是等腰三角形，所以A1M=A1C1=

2

．
如圖，將幾何體AA₁M-CC₁N補成三棱柱AA₁M-CC₁F
∴幾何體AA₁M-CC₁N的體積為：V1=

1

2

•AM•AA1•AC-

1

3

•

1

2

•CF•CC1•NF=

1

2

×1×1×

2

-

1

3

×

1

2

×1×1×

2

2

=

5 2

12

…（9分）
又直三棱柱ABC-A₁B₁C₁體積為：V=

1

2

×

2

×2×1=

2

…（11分）
故剩余的幾何體棱臺BMN-B₁A₁C₁的體積為：V2=V-V1=

7 2

12

∴較小部分的體積與較大部分體積之比為：

V1

V2

=

5

7

．                   …（12分）

點評：本題考查直線與平面平行的判定，棱柱、棱錐、棱臺的體積，根據題目條件，將問題靈活轉化是關鍵，考查邏輯推理能力與計算能力．