
【題目】已知函數f(x)= ![]() x2﹣alnx+
x2﹣alnx+ ![]() (a∈R) (Ⅰ)求函數f(x)單調區間;
(a∈R) (Ⅰ)求函數f(x)單調區間;
(Ⅱ)若a=﹣1,求證:當x>1時,f(x)< ![]() x3 .
x3 .
【答案】解:(Ⅰ)f(x)的定義域為x>0 ![]() 若a≤0時,f'(x)≥0恒成立,即f(x)的單調區間為(0,+∞)
若a≤0時,f'(x)≥0恒成立,即f(x)的單調區間為(0,+∞)
若a>0時,令f'(x)>0,得 ![]()
即f(x)的單調區間為 ![]() ,減區間為
,減區間為 ![]()
(Ⅱ)證明:設 ![]()
則 ![]()
∴F(x)在(1,+∞)上為增函數,且 ![]()
即F(x)>0在(1,+∞)上恒成立
∴當x>1, ![]()
【解析】(Ⅰ)求導數,分類討論,利用導數的正負求函數f(x)單調區間;(Ⅱ)設 ![]() ,證明F(x)在(1,+∞)上為增函數,即可得出結論.
,證明F(x)在(1,+∞)上為增函數,即可得出結論.
【考點精析】利用利用導數研究函數的單調性和函數的最大(小)值與導數對題目進行判斷即可得到答案,需要熟知一般的,函數的單調性與其導數的正負有如下關系: 在某個區間![]() 內,(1)如果
內,(1)如果![]() ,那么函數
,那么函數![]() 在這個區間單調遞增;(2)如果
在這個區間單調遞增;(2)如果![]() ,那么函數
,那么函數![]() 在這個區間單調遞減;求函數
在這個區間單調遞減;求函數![]() 在
在![]() 上的最大值與最小值的步驟:(1)求函數
上的最大值與最小值的步驟:(1)求函數![]() 在
在![]() 內的極值;(2)將函數
內的極值;(2)將函數![]() 的各極值與端點處的函數值
的各極值與端點處的函數值![]() ,
,![]() 比較,其中最大的是一個最大值,最小的是最小值.
比較,其中最大的是一個最大值,最小的是最小值.


 勵耘書業暑假銜接寧波出版社系列答案
勵耘書業暑假銜接寧波出版社系列答案科目:高中數學 來源: 題型:
【題目】曲線![]() 的參數方程為
的參數方程為![]() (
(![]() 為參數),以坐標原點為極點,
為參數),以坐標原點為極點, ![]() 軸的正半軸為極軸建立極坐標系,直線
軸的正半軸為極軸建立極坐標系,直線![]() 的極坐標方程為
的極坐標方程為![]() .
.
(1)寫出![]() 的直角坐標方程,并且用
的直角坐標方程,并且用![]() (
(![]() 為直線的傾斜角,
為直線的傾斜角, ![]() 為參數)的形式寫出直線
為參數)的形式寫出直線![]() 的一個參數方程;
的一個參數方程;
(2) ![]() 與
與![]() 是否相交,若相交求出兩交點的距離,若不相交,請說明理由.
是否相交,若相交求出兩交點的距離,若不相交,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在三棱錐D﹣ABC中,已知△BCD是正三角形,AB⊥平面BCD,AB=BC,E為BC的中點,F在棱AC上,且AF=3FC, 
(1)求證:AC⊥平面DEF;
(2)求平面DEF與平面ABD所成的銳二面角的余弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知0<k<4,直線l1:kx﹣2y﹣2k+8=0和直線l:2x+k2y﹣4k2﹣4=0與兩坐標軸圍成一個四邊形,則使得這個四邊形面積最小的k值為 .
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=loga(x﹣1),g(x)=loga(3﹣x)(a>0且a≠1)
(1)求函數h(x)=f(x)﹣g(x)的定義域;
(2)利用對數函數的單調性,討論不等式f(x)≥g(x)中x的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在四棱錐P﹣ABCD中,PA⊥底面ABCD,AB⊥AD,AC⊥CD,∠ABC=60°,PA=AB=BC,E是PC的中點. 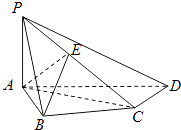
(1)證明CD⊥AE;
(2)證明PD⊥平面ABE; 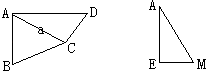
(3)求二面角A﹣PD﹣C的正切值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=log ![]() (3x2﹣ax+5)在[﹣1,+∞)上單調遞減,則實數a的取值范圍是( )
(3x2﹣ax+5)在[﹣1,+∞)上單調遞減,則實數a的取值范圍是( )
A.[﹣8,﹣6]
B.(﹣8,﹣6]
C.(﹣∞,﹣8)∪(﹣6,+∞)
D.(﹣∞,﹣6]
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】過雙曲線 ![]() =1(a>0,b>0)的左焦點F(﹣c,0)作圓x2+y2=a2的切線,切點為E,延長FE交拋物線y2=4cx于點P,O為坐標原點,若
=1(a>0,b>0)的左焦點F(﹣c,0)作圓x2+y2=a2的切線,切點為E,延長FE交拋物線y2=4cx于點P,O為坐標原點,若 ![]() =
= ![]() (
( ![]() +
+ ![]() ),則雙曲線的離心率為( )
),則雙曲線的離心率為( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com