
【題目】已知直線![]() ,閱讀如圖所示的程序框圖,若輸入的
,閱讀如圖所示的程序框圖,若輸入的![]() 的值為
的值為![]() ,輸出的
,輸出的![]() 的值恰為直線
的值恰為直線![]() 在
在![]() 軸上的截距,且
軸上的截距,且![]() .
.

(1)求直線![]() 與
與![]() 的交點坐標(biāo);
的交點坐標(biāo);
(2)若直線![]() 過直線
過直線![]() 與
與![]() 的交點,且在
的交點,且在![]() 軸上的截距是在
軸上的截距是在![]() 軸上的截距的2倍,求
軸上的截距的2倍,求![]() 的方程.
的方程.
【答案】(1)![]() ;(2)
;(2)![]() 或
或![]()
【解析】
(1)根據(jù)程序框圖,可得輸出的函數(shù)![]() ,由輸入
,由輸入![]() 的值為
的值為![]() 可得直線
可得直線![]() 在
在![]() 軸上的截距.由
軸上的截距.由![]() ,可得直線
,可得直線![]() 的斜率.根據(jù)點斜式可得直線
的斜率.根據(jù)點斜式可得直線![]() 的方程,聯(lián)立兩直線方程,即可求得交點坐標(biāo).
的方程,聯(lián)立兩直線方程,即可求得交點坐標(biāo).
(2)討論截距是否為0:當(dāng)截距為0時,易得直線方程;當(dāng)截距不為0時,根據(jù)在![]() 軸上的截距是在
軸上的截距是在![]() 軸上的截距的2倍,設(shè)出直線方程,代入所過的點,即可求解.
軸上的截距的2倍,設(shè)出直線方程,代入所過的點,即可求解.
(1)由程序框圖,若輸入![]() 的值為
的值為![]() ,由
,由![]()
所以輸出![]()
代入可得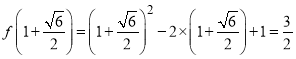
所以![]() 在
在![]() 軸上的截距為
軸上的截距為![]() ,
,
∵![]() ,
,
∴![]()
所以![]()
∴直線![]() 的方程為
的方程為![]() ,即
,即![]() .
.
聯(lián)立![]() ,解得
,解得![]() .
.
∴直線![]() 和
和![]() 的交點坐標(biāo)為
的交點坐標(biāo)為![]() .
.
(2)當(dāng)直線![]() 經(jīng)過原點時,可得方程為
經(jīng)過原點時,可得方程為![]() .
.
當(dāng)直線![]() 不經(jīng)過原點時,設(shè)在
不經(jīng)過原點時,設(shè)在![]() 軸上截距為
軸上截距為![]() ,則在
,則在![]() 軸上的截距為
軸上的截距為![]() ,
,
其方程為![]() ,將交點坐標(biāo)
,將交點坐標(biāo)![]() 代入可得
代入可得![]() ,解得
,解得![]() ,
,
∴方程為![]() .
.
綜上可得直線![]() 方程為
方程為![]() 或
或![]() .
.


 世紀(jì)百通主體課堂小學(xué)課時同步達(dá)標(biāo)系列答案
世紀(jì)百通主體課堂小學(xué)課時同步達(dá)標(biāo)系列答案 世紀(jì)百通優(yōu)練測系列答案
世紀(jì)百通優(yōu)練測系列答案 百分學(xué)生作業(yè)本題練王系列答案
百分學(xué)生作業(yè)本題練王系列答案科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知橢圓E:![]() +
+![]() =1(a>b>0)的離心率為
=1(a>b>0)的離心率為![]() ,焦點到相應(yīng)準(zhǔn)線的距離為
,焦點到相應(yīng)準(zhǔn)線的距離為![]() .
.
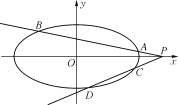
(1) 求橢圓E的標(biāo)準(zhǔn)方程;
(2) 已知P(t,0)為橢圓E外一動點,過點P分別作直線l1和l2,直線l1和l2分別交橢圓E于點A,B和點C,D,且l1和l2的斜率分別為定值k1和k2,求證:![]() 為定值.
為定值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)f(x)=4cos ωx·sin![]() +a(ω>0)圖象上最高點的縱坐標(biāo)為2,且圖象上相鄰兩個最高點的距離為π.
+a(ω>0)圖象上最高點的縱坐標(biāo)為2,且圖象上相鄰兩個最高點的距離為π.
(1)求a和ω的值;
(2)求函數(shù)f(x)在[0,π]上的單調(diào)遞減區(qū)間.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖,在平面直角坐標(biāo)系![]() 中,點
中,點![]() ,直線
,直線![]() ,設(shè)圓
,設(shè)圓![]() 的半徑為1, 圓心在
的半徑為1, 圓心在![]() 上.
上.

(1)若圓心![]() 也在直線
也在直線![]() 上,過點
上,過點![]() 作圓
作圓![]() 的切線,求切線方程;
的切線,求切線方程;
(2)若圓![]() 上存在點
上存在點![]() ,使
,使![]() ,求圓心
,求圓心![]() 的橫坐標(biāo)
的橫坐標(biāo)![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】給出下列命題:某射手射擊一次,擊中目標(biāo)的概率是0.9,他連續(xù)射擊三次,且他每次射擊是否擊中目標(biāo)之間沒有影響,有下列結(jié)論:①他三次都擊中目標(biāo)的概率是![]() ;②他第三次擊中目標(biāo)的概率是
;②他第三次擊中目標(biāo)的概率是![]() ; ③他恰好2次擊中目標(biāo)的概率是
; ③他恰好2次擊中目標(biāo)的概率是![]() ;④他至少
;④他至少![]() 次擊中目標(biāo)的概率是
次擊中目標(biāo)的概率是![]() ;⑤他至多2次擊中目標(biāo)的概率是
;⑤他至多2次擊中目標(biāo)的概率是![]() .其中正確命題的序號是 ________(正確命題的序號全填上).
.其中正確命題的序號是 ________(正確命題的序號全填上).
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】某市春節(jié)期間7家超市的廣告費支出![]() (萬元)和銷售額
(萬元)和銷售額![]() (萬元)數(shù)據(jù)如下:
(萬元)數(shù)據(jù)如下:
超市 | A | B | C | D | E | F | G |
廣告費支出 | 1 | 2 | 4 | 6 | 11 | 13 | 19 |
銷售額 | 19 | 32 | 40 | 44 | 52 | 53 | 54 |
參數(shù)數(shù)據(jù)及公式:![]() ,
,![]() ,
,![]() ,
,![]() ,
,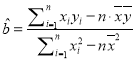 ,
,![]() ,
,![]() .
.
(1)若用線性回歸模型擬合y與x的關(guān)系,求y關(guān)于x的線性回歸方程;
(2)用對數(shù)回歸模型擬合y與x的關(guān)系,可得回歸方程:![]() ,經(jīng)計算得出線性回歸模型和對數(shù)模型的
,經(jīng)計算得出線性回歸模型和對數(shù)模型的![]() 分別約為0.75和0.97,請用
分別約為0.75和0.97,請用![]() 說明選擇哪個回歸模型更合適,并用此模型預(yù)測A超市廣告費支出為8萬元時的銷售額.
說明選擇哪個回歸模型更合適,并用此模型預(yù)測A超市廣告費支出為8萬元時的銷售額.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】在不超過2000的自然數(shù)中,任意選取601個數(shù).則這601個數(shù)中一定存在兩數(shù),其差為3或4或7.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】己知函數(shù)![]() .
.
(1)若f(x)有兩個極值點,求實數(shù)m的取值范圍:
(2)若函數(shù)![]() 有且只有三個不同的零點,分別記為x1,x2,x3,設(shè)x1<x2<x3,且
有且只有三個不同的零點,分別記為x1,x2,x3,設(shè)x1<x2<x3,且![]() 的最大值是e2,求x1x3的最大值.
的最大值是e2,求x1x3的最大值.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com