【題目】已知△ABC的三個內角A，B，C所對的邊分別為a，b，c. 
， 
，且 
．
（Ⅰ）求A的大小；
（Ⅱ）若a=1， 
．求S△ABC ．
開心快樂假期作業暑假作業西安出版社系列答案科目：高中數學 來源： 題型：
【題目】如圖，在三棱柱ABC﹣A1B1C1中，側面ABB1A1 ， ACC1A1均為正方形，AB=AC=1，∠BAC=90，點D是棱B1C1的中點．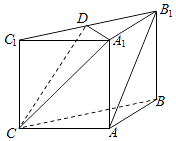 
（1）求證：AB1∥平面A1DC；
（2）求證：A1D⊥平面BB1C1C．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】選修4-4：坐標系與參數方程
在平面直角坐標系
中，曲線
： 
，曲線
： 
（
為參數），以坐標原點
為極點， 
軸正半軸為極軸，建立極坐標系.
（Ⅰ）求曲線
， 
的極坐標方程；
（Ⅱ）曲線
： 
（
為參數， 
， 
）分別交
， 
于
， 
兩點，當
取何值時， 
取得最大值.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知橢圓
，與
軸的正半軸交于點
，右焦點
， 
為坐標原點，且
．
（1）求橢圓的離心率
；
（2）已知點
，過點
任意作直線
與橢圓
交于
兩點，設直線
的斜率
，若
，求橢圓
的方程．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知
，且
，設命題p：函數
在
上單調遞減；命題q：函數
在
上為增函數，
（1）若“p且q”為真，求實數c的取值范圍
（2）若“p且q”為假，“p或q”為真，求實數c的取值范圍．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】襄陽農科所對冬季晝夜溫差大小與某反季節大豆新品種發芽多少之間的關系進行分析研究，他們分別記錄了12月1日至12月5日的每天晝夜溫度與實驗室每天每100顆種子中的發芽數，得到如下數據：
襄陽農科所確定的研究方案是：先從這5組數據中選取2組，用剩下的3組數據求線性回歸方程，再對被選取的2組數據進行檢驗.
（1）求選取的2組數據恰好是不相鄰的2天數據的概率；
（2）若選取的是12月1日與12月5日這兩組數據，情根據12月2日至12月4日的數據，求
關于
的線性回歸方程
；
（3）若由線性回歸方程得到的估計數據與所選出的檢驗數據的誤差均不超過1顆，則認為得到的線性回歸方程是可靠的，試問（2）中所得的線性回歸方程是否可靠？
注：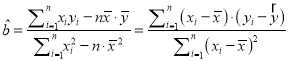 
， 
.
查看答案和解析>>
科目：高中數學 來源： 題型：
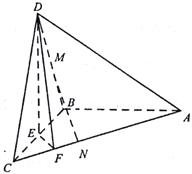
【題目】如圖,在三棱錐D-ABC中,已知△BCD是正三角形,AB⊥平面BCD,AB=BC=a,E為BC的中點,F在棱AC上,且AF=3FC
(1)求三棱錐D-ABC的體積
(2)求證:平面DAC⊥平面DEF;
(3)若M為DB中點,N在棱AC上,且CN=
CA,求證:MN∥平面DEF
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】我國古代數學名著《算法統宗》中有如下問題：“遠望巍巍塔七層，紅光點點倍加增，共燈三百八十一，請問尖頭幾盞燈？”意思是：一座7層塔共掛了381盞燈，且相鄰兩層中的下一層燈數是上一層燈數的2倍，則塔的頂層共有燈（ ）
A. 1盞 B. 3盞 C. 5盞 D. 9盞
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某公司為了準確地把握市場，做好產品生產計劃，對過去四年的數據進行整理得到了第
年與年銷量
（單位：萬件）之間的關系如下表：
（1）在圖中畫出表中數據的散點圖；
（2）根據散點圖選擇合適的回歸模型擬合
與
的關系（不必說明理由）；
（3）建立
關于
的回歸方程，預測第5年的銷售量.
附注：參考公式：回歸直線的斜率和截距的最小二乘法估計公式分別為：
， 
.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
