
【題目】已知函數(shù) F (x) = e x 滿足 F ( x) = g ( x) + h( x) ,且 g ( x), h( x) 分別是定義在 R 上的偶函數(shù)和奇函數(shù).
(1)求函數(shù) h(x)的反函數(shù);
(2)已知(x) = g(x 1),若函數(shù)(x)在 [1,3]上滿足(2 a+1) ![]() ,求實(shí)數(shù) a 的取值范圍;
,求實(shí)數(shù) a 的取值范圍;
(3)若對于任意 x ∈(0,2]不等式 g(2x) ah(x) ≥ 0 恒成立,求實(shí)數(shù) a 的取值范圍.
【答案】(1)![]() (2)
(2)![]() (3)
(3)![]()
【解析】
(1)由題意可得:![]() ,
,![]() ,聯(lián)立解得:
,聯(lián)立解得:![]() ,
,![]() .由
.由![]() ,化為:
,化為:![]() ,
,![]() ,解得
,解得![]() .可得
.可得![]() .
.
(2)![]() ,函數(shù)
,函數(shù)![]() 在
在![]() ,
,![]() 上滿足
上滿足![]() ,轉(zhuǎn)化為:函數(shù)
,轉(zhuǎn)化為:函數(shù)![]() 在
在![]() ,
,![]() 上滿足:
上滿足:![]() ,由于函數(shù)
,由于函數(shù)![]() 在
在![]() ,
,![]() 上單調(diào)遞增,且函數(shù)
上單調(diào)遞增,且函數(shù)![]() 為偶函數(shù),可得
為偶函數(shù),可得![]() ,
,![]() ,
,![]() ,解得
,解得![]() 范圍.
范圍.
(3)不等式![]() ,即
,即![]() ,令
,令![]() ,由
,由![]() ,
,![]() ,可得
,可得![]() ,
,![]() ,不等式轉(zhuǎn)化為:
,不等式轉(zhuǎn)化為:![]() ,
,![]() ,利用基本不等式的性質(zhì)即可得出.
,利用基本不等式的性質(zhì)即可得出.
解:(1)由題意可得:![]() ,
,![]() ,
,
聯(lián)立解得:![]() ,
,![]() .
.
由![]() ,化為:
,化為:![]() ,
,![]() ,解得
,解得![]() .
.
![]() .
.
(2)![]() ,函數(shù)
,函數(shù)![]() 在
在![]() ,
,![]() 上滿足
上滿足![]() ,
,
轉(zhuǎn)化為:函數(shù)![]() 在
在![]() ,
,![]() 上滿足:
上滿足:![]() ,
,
由于函數(shù)![]() 在
在![]() ,
,![]() 上單調(diào)遞增,且函數(shù)
上單調(diào)遞增,且函數(shù)![]() 為偶函數(shù),
為偶函數(shù),
![]() ,
,![]() ,
,![]() ,解得
,解得![]() .
.
(3)不等式![]() ,即
,即![]() ,
,
令![]() ,由
,由![]() ,
,![]() ,可得
,可得![]() ,
,![]() ,
,
不等式轉(zhuǎn)化為:![]() ,
,![]() ,
,![]() ,當(dāng)且僅當(dāng)
,當(dāng)且僅當(dāng)![]() 時(shí)取等號.
時(shí)取等號.
![]() .
.



| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:
【題目】朱載堉(1536—1611),明太祖九世孫,音樂家、數(shù)學(xué)家、天文歷算家,在他多達(dá)百萬字的著述中以《樂律全書》最為著名,在西方人眼中他是大百科全書式的學(xué)者王子。他對文藝的最大貢獻(xiàn)是他創(chuàng)建了“十二平均律”,此理論被廣泛應(yīng)用在世界各國的鍵盤樂器上,包括鋼琴,故朱載堉被譽(yù)為“鋼琴理論的鼻祖”。“十二平均律”是指一個(gè)八度有13個(gè)音,相鄰兩個(gè)音之間的頻率之比相等,且最后一個(gè)音頻率是最初那個(gè)音頻率的2倍,設(shè)第二個(gè)音的頻率為![]() ,第八個(gè)音的頻率為
,第八個(gè)音的頻率為![]() ,則
,則![]() 等于( )
等于( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知![]() ,
,![]() 分別為雙曲線
分別為雙曲線![]()
![]()
![]() 的左、右焦點(diǎn),點(diǎn)P是以
的左、右焦點(diǎn),點(diǎn)P是以![]() 為直徑的圓與C在第一象限內(nèi)的交點(diǎn),若線段
為直徑的圓與C在第一象限內(nèi)的交點(diǎn),若線段![]() 的中點(diǎn)Q在C的漸近線上,則C的兩條漸近線方程為__________.
的中點(diǎn)Q在C的漸近線上,則C的兩條漸近線方程為__________.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】“移動(dòng)支付、高鐵、網(wǎng)購、共享單車”被稱為中國的“新四大發(fā)明”.為了幫助50歲以上的中老年人更快地適應(yīng)“移動(dòng)支付”,某機(jī)構(gòu)通過網(wǎng)絡(luò)組織50歲以上的中老年人學(xué)習(xí)移動(dòng)支付相關(guān)知識.學(xué)習(xí)結(jié)束后,每人都進(jìn)行限時(shí)答卷,得分都在![]() 內(nèi).在這些答卷(有大量答卷)中,隨機(jī)抽出
內(nèi).在這些答卷(有大量答卷)中,隨機(jī)抽出![]() 份,統(tǒng)計(jì)得分繪出頻率分布直方圖如圖.
份,統(tǒng)計(jì)得分繪出頻率分布直方圖如圖.
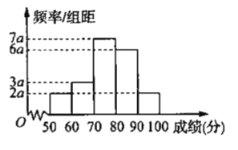
(1)求出圖中![]() 的值,并求樣本中,答卷成績在
的值,并求樣本中,答卷成績在![]() 上的人數(shù);
上的人數(shù);
(2)以樣本的頻率為概率,從參加這次答卷的人群中,隨機(jī)抽取![]() 名,記成績在
名,記成績在![]() 分以上(含
分以上(含![]() 分)的人數(shù)為
分)的人數(shù)為![]() ,求
,求![]() 的分布列和期望.
的分布列和期望.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖,在地上有同樣大小的 5 塊積木,一堆 2 個(gè),一堆 3 個(gè),要把積木一塊一塊的全部放到某個(gè)盒子里,每次 只能取出其中一堆最上面的一塊,則不同的取法有______種(用數(shù)字作答).
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】設(shè)函數(shù)![]() ,函數(shù)
,函數(shù)![]() ,
,![]() ,其中
,其中![]() 為常數(shù),且
為常數(shù),且![]() ,令函數(shù)
,令函數(shù)![]() 為函數(shù)
為函數(shù)![]() 和
和![]() 的積函數(shù).
的積函數(shù).
(1)求函數(shù)![]() 的表達(dá)式,并求其定義域;
的表達(dá)式,并求其定義域;
(2)當(dāng)![]() 時(shí),求函數(shù)
時(shí),求函數(shù)![]() 的值域
的值域
(3)是否存在自然數(shù)![]() ,使得函數(shù)
,使得函數(shù)![]() 的值域恰好為
的值域恰好為![]() ?若存在,試寫出所有滿足條件的自然數(shù)
?若存在,試寫出所有滿足條件的自然數(shù)![]() 所構(gòu)成的集合;若不存在,試說明理由.
所構(gòu)成的集合;若不存在,試說明理由.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖,在四棱錐P-ABCD中,底面ABCD為平行四邊形,點(diǎn)O為對角線BD的中點(diǎn),點(diǎn)E,F(xiàn)分別為棱PC,PD的中點(diǎn),已知PA⊥AB,PA⊥AD.
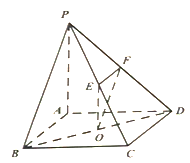
(1)求證:直線PB∥平面OEF;
(2)求證:平面OEF⊥平面ABCD.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】設(shè)![]() ,其中
,其中![]() ,函數(shù)
,函數(shù)![]() 在點(diǎn)
在點(diǎn)![]() 處的切線方程為
處的切線方程為![]() ,其中
,其中![]() .
.
(1)求![]() 和
和![]() 并證明函數(shù)
并證明函數(shù)![]() 有且僅有一個(gè)零點(diǎn);
有且僅有一個(gè)零點(diǎn);
(2)當(dāng)![]() 時(shí),
時(shí),![]() 恒成立,求最小的整數(shù)
恒成立,求最小的整數(shù)![]() 的值.
的值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】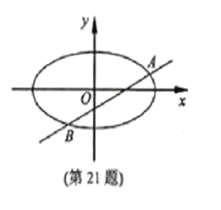
(本題滿分15分)已知m>1,直線![]() ,
,
橢圓![]() ,
,![]() 分別為橢圓
分別為橢圓![]() 的左、右焦點(diǎn).
的左、右焦點(diǎn).
(Ⅰ)當(dāng)直線![]() 過右焦點(diǎn)
過右焦點(diǎn)![]() 時(shí),求直線
時(shí),求直線![]() 的方程;
的方程;
(Ⅱ)設(shè)直線![]() 與橢圓
與橢圓![]() 交于
交于![]() 兩點(diǎn),
兩點(diǎn),![]() ,
,
![]() 的重心分別為
的重心分別為![]() .若原點(diǎn)
.若原點(diǎn)![]() 在以線段
在以線段
![]() 為直徑的圓內(nèi),求實(shí)數(shù)
為直徑的圓內(nèi),求實(shí)數(shù)![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺 | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com