【題目】在如圖所示的圓臺中，AC是下底面圓O的直徑，EF是上底面圓O
的直徑，FB是圓臺的一條母線.
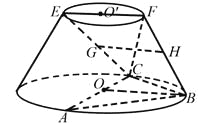
（Ⅰ）已知G,H分別為EC，FB的中點，求證：GH∥平面ABC；
（Ⅱ）已知EF=FB=
AC=
，AB=BC.求二面角
的余弦值.
【答案】（Ⅰ）見解析；（Ⅱ） 
【解析】試題分析：（Ⅰ）取
中點
，連結
，推導出平面
平面
，由此能證明
平面
；（Ⅱ）由
，知
，以
為原點， 
為
軸， 
為
軸， 
為
軸，建立空間直角坐標系，利用向量法能求出二面角
的余弦值．
試題解析：(Ⅰ)連結
，取
的中點
，連結
， 
， 
、
在上底面內， 
不在上底面內， 
上底面，………………2分
平面
，又
， 
平面
， 
平面
，
平面
，………………4分
所以平面
平面
，由
平面
， 
平面
．………………5分
(Ⅱ)連結
， 
， 
，………………6分
以
為原點，分別以
， 
， 
為
， 
， 
軸建立空間直角坐標系，
， 
， 
，
于是有
， 
， 
， 
，
可得平面
中的向量
， 
，于是得平面
的一個法向量
，………………9分
又平面
的一個法向量
………………10分
設二面角
為
，則
，
二面角
的余弦值為
………………12分
科目：高中數學 來源： 題型：
【題目】已知橢圓
的左、右焦點分別為
，離心率為
，直線
與
的兩個交點間的距離為
.
（Ⅰ）求橢圓的方程；
（Ⅱ）分別過作
滿足
，設與的上半部分分別交于
兩點，求四邊形
面積的最大值.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知函數
.
（Ⅰ）求方程
的實數解；
（Ⅱ）如果數列
滿足
，
（
），是否存在實數
，使得
對所有的都成立？證明你的結論．
（Ⅲ）在（Ⅱ）的條件下，設數列的前
項的和為
，證明：
．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】莫言是中國首位獲得諾貝爾文學獎的文學家，國人歡欣鼓舞。某高校文學社從男女生中各抽取50名同學調查對莫言作品的了程度，結果如下：
閱讀過莫言的作品數（篇） | 0～25 | 26～50 | 51～75 | 76～100 | 101～130 |
男生 | 3 | 6 | 11 | 18 | 12 |
女生 | 4 | 8 | 13 | 15 | 10 |
（1）試估計該學校學生閱讀莫言作品超過50篇的概率.
（2）對莫言作品閱讀超過75篇的則稱為“對莫言作品非常了解”，否則為“一般了解”，根據題意完成下表，并判斷能否有
的把握認為“對莫言作品的非常了解”與性別有關？
非常了解 | 一般了解 | 合計 | |
男生 | |||
女生 | |||
合計 |
注：K2＝
P(K2≥k0) | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 |
k0 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 |
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖，嵩山上原有一條筆直的山路BC，現在又新架設了一條索道AC，小李在山腳B處看索道AC，發現張角∠ABC＝120°；從B處攀登400米到達D處，回頭看索道AC，發現張角∠ADC＝150°；從D處再攀登800米方到達C處，則索道AC的長為________米.
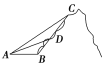
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某城市理論預測2000年到2004年人口總數與年份的關系如下表所示
年份200 | 0 | 1 | 2 | 3 | 4 |
人口數 | 5 | 7 | 8 | 11 | 19 |
（1）請畫出上表數據的散點圖；
（2）請根據上表提供的數據，用最小二乘法求出
關于
的線性回歸方程；
（3）據此估計2005年該城市人口總數.
參考公式： 用最小二乘法求線性回歸方程系數公式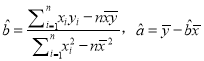 
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖所示，一個圓柱形乒乓球筒，高為
厘米，底面半徑為
厘米.球筒的上底和下底分別粘有一個乒乓球，乒乓球與球筒底面及側面均相切（球筒和乒乓球厚度忽略不計）.一個平面與兩乒乓球均相切，且此平面截球筒邊緣所得的圖形為一個橢圓，則該橢圓的離心率為（ ）
A. 
B. 
C. 
D. 
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
