
【題目】已知定義在R上的函數![]() 對任意實數
對任意實數![]() 都滿足
都滿足![]() ,且當
,且當![]() 時,
時,![]() .
.
(1)判斷函數![]() 的奇偶性,并證明;
的奇偶性,并證明;
(2)判斷函數![]() 的單調性,并證明;
的單調性,并證明;
(3)解不等式![]() .
.
【答案】(1)![]() 為奇函數.證明見解析(2)
為奇函數.證明見解析(2)![]() 在R上為增函數.證明見解析(3)當
在R上為增函數.證明見解析(3)當![]() 時不等式的解集是
時不等式的解集是![]() .當
.當![]() 時不等式的解集是
時不等式的解集是![]() .當
.當![]() 時不等式的解集是
時不等式的解集是![]() .
.
【解析】
(1)用賦值法求出![]() ,然后令
,然后令![]() 可得奇偶性;
可得奇偶性;
(2)利用單調性的定義證明單調性;
(3)由奇函數性質化不等式為![]() ,由單調性轉化為二次不等式,再分類得出解集.
,由單調性轉化為二次不等式,再分類得出解集.
(1)解:![]() 為奇函數.
為奇函數.
證明:因為![]() ,令
,令![]() ,
,
得![]() 對任意的
對任意的![]() 都成立,所以
都成立,所以![]() .
.
又令![]() ,則
,則![]() ,
,
所以![]() ,所以
,所以![]() 是奇函數.
是奇函數.
(2)解:![]() 在R上為增函數.
在R上為增函數.
證明:![]() ,且使
,且使![]() 由
由![]() 是奇函數,
是奇函數,
得![]() .
.
因為當![]() 時,
時,![]() ,
,
而![]() ,所以
,所以![]() ,
,
所以![]() ,所以
,所以![]() 在R上為增函數.
在R上為增函數.
(3)解:由![]() ,得
,得![]() .
.
因為![]() 是奇函數,所以
是奇函數,所以![]() .
.
又![]() 在R上為增函數,所以
在R上為增函數,所以![]() .
.
即![]() ,所以
,所以![]() .
.
所以當![]() 時不等式的解集是
時不等式的解集是![]() .
.
當![]() 時不等式的解集是
時不等式的解集是![]() .
.
當![]() 時不等式的解集是
時不等式的解集是![]() .
.


科目:高中數學 來源: 題型:
【題目】已知函數f(x)是定義在R上的奇函數,當x>0時,![]() .
.
(1)求f(x)的解析式;
(2)設x∈[1,2]時,函數![]() ,是否存在實數m使得g(x)的最小值為6,若存在,求m的取值;若不存在,說明理由.
,是否存在實數m使得g(x)的最小值為6,若存在,求m的取值;若不存在,說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某公司在過去幾年內使用某種型號的燈管1 000根,該公司對這些燈管的使用壽命(單位:h)進行了統計,統計結果如表所示:
分組 |
|
|
|
|
頻數 | 48 | 121 | 208 | 223 |
頻率 | ||||
分組 |
|
|
| |
頻數 | 193 | 165 | 42 | |
頻率 |
(1)將各組的頻率填入表中;
(2)根據上述統計結果,估計該種型號燈管的使用壽命不足1500 h的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某學校為了了解學生使用手機的情況,分別在高一和高二兩個年級各隨機抽取了100名學生進行調查.下面是根據調查結果繪制的學生日均使用手機時間的頻數分布表和頻率分布直方圖,將使用手機時間不低于80分鐘的學生稱為“手機迷”.
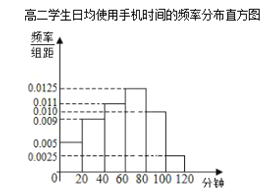
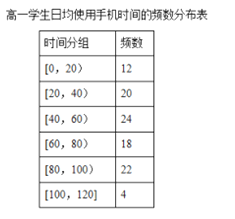
(I)將頻率視為概率,估計哪個年級的學生是“手機迷”的概率大?請說明理由.
(II)在高二的抽查中,已知隨機抽到的女生共有55名,其中10名為“手機迷”.根據已知條件完成下面的2×2列聯表,并據此資料你有多大的把握認為“手機迷”與性別有關?
非手機迷 | 手機迷 | 合計 | |
男 | |||
女 | |||
合計 |
附:隨機變量![]() (其中
(其中![]() 為樣本總量).
為樣本總量).
參考數據 |
| 0.15 | 0.10 | 0.05 | 0.025 |
| span>2.072 | 2.706 | 3.841 | 5.024 |
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知集合A={x|2≤x≤8},B={x|1<x<6},C={x|x>a},U=R.
(1)求A∪B,(CUA)∩B;
(2)若A∩C≠![]() ,求a的取值范圍.
,求a的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在正四棱錐S-ABCD中,E,M,N分別是BC,CD,SC的中點,動點P在線段MN上運動時,下列四個結論:①EP⊥AC;②EP∥BD;③EP∥平面SBD;④EP⊥平面SAC,其中恒成立的為( )
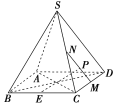
A.①③B.③④C.①②D.②③④
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】(本小題共13分)
如圖,正方形ABCD和四邊形ACEF所在的平面互相垂直。
EF//AC,AB=![]() ,CE=EF=1
,CE=EF=1
(Ⅰ)求證:AF//平面BDE;
(Ⅱ)求證:CF⊥平面BDF;
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】“開門大吉”是某電視臺推出的游戲節目,選手面對1~8號8扇大門,依次按響門上的門鈴,門鈴會播放一段音樂(將一首經典流行歌曲以單音色旋律的方式演繹),選手需正確回答出這首歌的名字,方可獲得該扇門對應的家庭夢想基金.在一次場外調查中,發現參賽選手多數分為兩個年齡段:20~30;30~40(單位:歲).其猜對歌曲名稱與否的人數如圖所示.
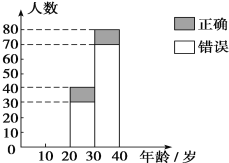
(1)寫出2×2列聯表;判斷能否在犯錯誤的概率不超過0.10的前提下認為猜對歌曲名稱與年齡有關系,說明你的理由.(下面的臨界值表供參考)
P(K2≥k0) | 0.10 | 0.05 | 0.010 | 0.005 |
k0 | 2.706 | 3.841 | 6.635 | 7.879 |
(2)現計劃在這次場外調查中按年齡段用分層抽樣的方法選取6名選手,求20~30歲與30~40歲各有幾人.
參考公式:K2=![]() ,其中n=a+b+c+d.
,其中n=a+b+c+d.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com