
【題目】如圖,漁船甲位于島嶼A的南偏西60°方向的B處,且與島嶼A相距12海里,漁船乙以10海里/小時的速度從島嶼A出發沿正北方向航行,若漁船甲同時從B處出發沿北偏東α的方向追趕漁船乙,剛好用2小時追上. 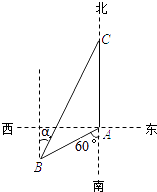
(1)求漁船甲的速度;
(2)求sinα的值.
【答案】
(1)解:依題意,∠BAC=120°,AB=12,AC=10×2=20,∠BCA=α.在△ABC中,由余弦定理,得BC2=AB2+AC2﹣2AB×AC×cos∠BAC
=122+202﹣2×12×20×cos120°=784.
解得BC=28.
所以漁船甲的速度為 ![]() 海里/小時.
海里/小時.
答:漁船甲的速度為14海里/小時
(2)解:方法1:在△ABC中,因為AB=12,∠BAC=120°,BC=28,∠BCA=α,
由正弦定理,得 ![]() .
.
即 ![]() .
.
答:sinα的值為 ![]() .
.
方法2:在△ABC中,因為AB=12,AC=20,BC=28,∠BCA=α,
由余弦定理,得 ![]() .
.
即 ![]() .
.
因為α為銳角,所以 ![]() =
= ![]() .
.
答:sinα的值為 ![]()
【解析】(1)由題意推出∠BAC=120°,利用余弦定理求出BC=28,然后推出漁船甲的速度;(2)方法一:在△ABC中,直接利用正弦定理求出sinα.方法二:在△ABC中,利用余弦定理求出cosα,然后轉化為sinα.


 名校課堂系列答案
名校課堂系列答案科目:高中數學 來源: 題型:
【題目】橢圓![]() +
+![]() =1的左、右焦點分別為F1,F2,一條直線
=1的左、右焦點分別為F1,F2,一條直線![]() 經過點F1與橢圓交于A,B兩點.
經過點F1與橢圓交于A,B兩點.
(1)求△ABF2的周長;
(2)若![]() 的傾斜角為
的傾斜角為![]() ,求弦長|AB|.
,求弦長|AB|.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設函數![]() 的定義域均為
的定義域均為![]() ,且
,且![]() 是奇函數,
是奇函數,![]() 是偶函數,
是偶函數,![]() ,其中
,其中![]() 為自然對數的底數.
為自然對數的底數.
(1)求![]() 的解析式,并證明:當
的解析式,并證明:當![]() 時,
時,![]() ;
;
(2)若關于![]() 的不等式
的不等式![]() 在
在![]() 上恒成立,求實數
上恒成立,求實數![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】下表提供了某廠節能降耗技術改造后生產甲產品過程中記錄的產量(![]() 噸)與相應的生產能耗
噸)與相應的生產能耗![]() (噸)標準煤的幾組對照數據:
(噸)標準煤的幾組對照數據:
|
|
|
|
|
|
|
|
|
|
(1)請畫出上表數據的散點圖;并指出![]() 是否線性相關;
是否線性相關;
(2)請根據上表提供的數據,用最小二乘法求出![]() 關于
關于![]() 的線性回歸方程
的線性回歸方程![]()
![]() ;
;
(3)已知該廠技術改造前![]() 噸甲產品能耗為
噸甲產品能耗為![]() 噸標準煤,試根據求出的線性回歸方程,預測生產
噸標準煤,試根據求出的線性回歸方程,預測生產![]() 噸甲產品的生產能耗比技術改造前降低多少噸標準煤?
噸甲產品的生產能耗比技術改造前降低多少噸標準煤?
(參考:用最小二乘法求線性回歸方程系數公式 ,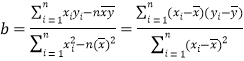 ,
, ![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=Asin(ωx+φ),x∈R(其中A>0,ω>0,0<φ< ![]() )的圖象與x軸的交點中,相鄰兩個交點之間的距離為
)的圖象與x軸的交點中,相鄰兩個交點之間的距離為 ![]() ,且圖象上一個最高點為M(
,且圖象上一個最高點為M( ![]() ,3).
,3).
(1)求f(x)的解析式;
(2)先把函數y=f(x)的圖象向左平移 ![]() 個單位長度,然后再把所得圖象上各點的橫坐標伸長到原來的2倍(縱坐標不變),得到函數y=g(x)的圖象,試寫出函數y=g(x)的解析式.
個單位長度,然后再把所得圖象上各點的橫坐標伸長到原來的2倍(縱坐標不變),得到函數y=g(x)的圖象,試寫出函數y=g(x)的解析式.
(3)在(2)的條件下,若總存在x0∈[﹣ ![]() ,
, ![]() ],使得不等式g(x0)+2≤log3m成立,求實數m的最小值.
],使得不等式g(x0)+2≤log3m成立,求實數m的最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知一個幾何體的三視圖如圖所示.

(1)求此幾何體的表面積;
(2)如果點![]() 在正視圖中所示位置:
在正視圖中所示位置:![]() 為所在線段中點,
為所在線段中點,![]() 為頂點,求在幾何體表面上,從
為頂點,求在幾何體表面上,從![]() 點到
點到![]() 點的最短路徑的長.
點的最短路徑的長.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=sin(ωx+)(ω>0,0≤≤π)為偶函數,其圖象上相鄰的兩個最高點之間的距離為2π.
(1)求f(x)的解析式;
(2)若 ![]() ,求
,求 ![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某廠有4臺大型機器,在一個月中,一臺機器至多出現1次故障,且每臺機器是否出現故障是相互獨立的,出現故障時需1名工人進行維修,每臺機器出現故障需要維修的概率為![]() .
.
(1)若出現故障的機器臺數為![]() ,求
,求![]() 的分布列;
的分布列;
(2) 該廠至少有多少名工人才能保證每臺機器在任何時刻同時出現故障時能及時進行維修的概率不少于90%?
(3)已知一名工人每月只有維修1臺機器的能力,每月需支付給每位工人1萬元的工資,每臺機器不出現故障或出現故障能及時維修,就使該廠產生5萬元的利潤,否則將不產生利潤,若該廠現有2名工人,求該廠每月獲利的均值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com