
【題目】橢圓![]() +
+![]() =1的左、右焦點分別為F1,F(xiàn)2,一條直線
=1的左、右焦點分別為F1,F(xiàn)2,一條直線![]() 經(jīng)過點F1與橢圓交于A,B兩點.
經(jīng)過點F1與橢圓交于A,B兩點.
(1)求△ABF2的周長;
(2)若![]() 的傾斜角為
的傾斜角為![]() ,求弦長|AB|.
,求弦長|AB|.
【答案】(1)8(2)![]()
【解析】試題分析:解決橢圓問題要注意“勿忘定義”,根據(jù)橢圓的定義,把三角形周長看成點A到兩焦點的距離和及點B到兩焦點距離和,求橢圓的弦長利用弦長公式,一般設而不求,把直線方程和橢圓方程聯(lián)立方程組,借助根與系數(shù)的關系,利用![]() 和
和![]() 求弦長.
求弦長.
試題解析:
(1)橢圓![]() ,a=2,b=
,a=2,b=![]() ,c=1,
,c=1,
由橢圓的定義,得丨AF1丨+丨AF2丨=2a=4,丨BF1丨+丨BF2丨=2a=4,
又丨AF1丨+丨BF1丨=丨AB丨,
∴△ABF2的周長為![]()
∴故△ABF2點周長為8;
(2)由(1)可知,得F1(﹣1,0),
∵AB的傾斜角為![]() ,則AB斜率為1,A(x1,y1),B(x2,y2),
,則AB斜率為1,A(x1,y1),B(x2,y2),
故直線AB的方程為y=x+1. 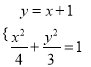 ,整理得:7y2﹣6y﹣9=0,
,整理得:7y2﹣6y﹣9=0,
由韋達定理可知:y1+y2=![]() ,y1y2=﹣
,y1y2=﹣![]() ,
,
則由弦長公式丨AB丨=![]()
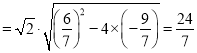 ,
,
弦長|AB|=![]() .
.


科目:高中數(shù)學 來源: 題型:
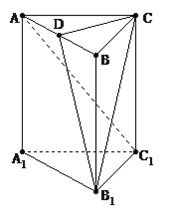
【題目】如圖,在直三棱柱ABC-A1B1C1中,AC=BC=CC1,AC⊥BC, 點D是AB的中點.
(Ⅰ)求證:CD⊥平面A1ABB1;
(Ⅱ)求證:AC1∥平面CDB1;
(Ⅲ)線段AB上是否存在點M,使得A1M⊥平面CDB1?
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】定義在區(qū)間![]() 上的函數(shù)
上的函數(shù)![]() 和
和![]() ,如果對任意
,如果對任意![]() ,都有
,都有![]() 成立,則稱
成立,則稱![]() 在區(qū)間
在區(qū)間![]() 上可被
上可被![]() 替代,
替代, ![]() 稱為“替代區(qū)間”.給出以下問題:
稱為“替代區(qū)間”.給出以下問題:
①![]() 在區(qū)間
在區(qū)間![]() 上可被
上可被![]() 替代;
替代;
②如果![]() 在區(qū)間
在區(qū)間![]() 可被
可被![]() 替代,則
替代,則![]() ;
;
③設![]() ,則存在實數(shù)
,則存在實數(shù)![]() 及區(qū)間
及區(qū)間![]() , 使得
, 使得![]() 在區(qū)間
在區(qū)間![]() 上被
上被![]() 替代.
替代.
其中真命題是
A. ①②③ B. ②③ C. ①③ D. ①②
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知橢圓![]() 經(jīng)過點
經(jīng)過點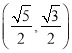 ,離心率為
,離心率為![]() ,點
,點![]() 坐標原點.
坐標原點.
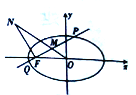
(1)求橢圓![]() 的標準方程;
的標準方程;
(2)過橢圓![]() 的左焦點
的左焦點![]() 任作一條不垂直于坐標軸的直線
任作一條不垂直于坐標軸的直線![]() ,交橢圓
,交橢圓![]() 于
于![]() 兩點,記弦
兩點,記弦![]() 的中點為
的中點為![]() ,過
,過![]() 作
作![]() 的垂線
的垂線![]() 交直線
交直線![]() 于點
于點![]() ,證明:點
,證明:點![]() 在一條定直線上.
在一條定直線上.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知數(shù)列{an}是首項為a1=![]() ,公比q=
,公比q=![]() 的等比數(shù)列,設
的等比數(shù)列,設![]() ,數(shù)列
,數(shù)列![]() 滿足cn=an·bn.
滿足cn=an·bn.
(1)求證:{bn}是等差數(shù)列;
(2)求數(shù)列{cn}的前n項和Sn;
(3)若cn≤![]() m2+m-1對一切正整數(shù)n恒成立,求實數(shù)m的取值范圍.
m2+m-1對一切正整數(shù)n恒成立,求實數(shù)m的取值范圍.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
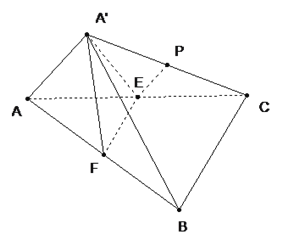
【題目】如圖, ![]() 、
、![]() 分別為直角三角形
分別為直角三角形![]() 的直角邊
的直角邊![]() 和斜邊
和斜邊![]() 的中點,沿
的中點,沿![]() 將
將![]() 折起到
折起到![]() 的位置,連結
的位置,連結![]() 、
、![]() ,
, ![]() 為
為![]() 的中點.
的中點.
(1)求證: ![]() 平面
平面![]() ;(2)求證:平面
;(2)求證:平面![]() 平面
平面![]() ;
;
(3)求證: ![]() 平面
平面![]() .
.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】如圖,漁船甲位于島嶼A的南偏西60°方向的B處,且與島嶼A相距12海里,漁船乙以10海里/小時的速度從島嶼A出發(fā)沿正北方向航行,若漁船甲同時從B處出發(fā)沿北偏東α的方向追趕漁船乙,剛好用2小時追上. 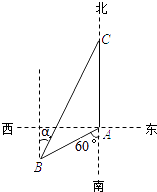
(1)求漁船甲的速度;
(2)求sinα的值.
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com