
【題目】如圖,四面體ABCD中,O是BD的中點,AB=AD=2,![]() .
.

(1)求證:AO⊥平面BCD;
(2)求異面直線AD與BC所成角的余弦值的大小;
科目:高中數學 來源: 題型:
【題目】下列四個說法中,錯誤的選項有( ).
A.若函數![]() 在
在![]() 上是單調增函數,在
上是單調增函數,在![]() 上也是單調增函數,則函數
上也是單調增函數,則函數![]() 在R上是單調增函數
在R上是單調增函數
B.已知函數的解析式為![]() ,它的值域為
,它的值域為![]() ,這樣的函數有無數個
,這樣的函數有無數個
C.把函數![]() 的圖像向右平移
的圖像向右平移![]() 個單位長度,就得到了函數
個單位長度,就得到了函數![]() 的圖像
的圖像
D.若函數![]() 為奇函數,則一定有
為奇函數,則一定有![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() ,
,![]() .
.
(1)若![]() ,且直線
,且直線![]() 是曲線
是曲線![]() 的一條切線,求實數
的一條切線,求實數![]() 的值;
的值;
(2)若不等式![]() 對任意
對任意![]() 恒成立,求
恒成立,求![]() 的取值范圍;
的取值范圍;
(3)若函數![]() 有兩個極值點
有兩個極值點![]() ,
,![]() ,且
,且![]() ,求
,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】進入12月以業,在華北地區連續出現兩次重污染天氣的嚴峻形勢下,我省堅持保民生,保藍天,各地嚴格落實機動車限行等一系列“管控令”,某市交通管理部門為了了解市民對“單雙號限行”的態度,隨機采訪了200名市民,將他們的意見和是否擁有私家車的情況進行了統計,得到如下的![]() 列聯表:
列聯表:
贊同限行 | 不贊同限行 | 合計 | |
沒有私家車 | 90 | 20 | 110 |
有私家車 | 70 | 40 | 110 |
合計 | 160 | 60 | 220 |
(1)根據上面的列聯表判斷能否在犯錯誤的概率不超過![]() 的前提下認為“對限行的態度與是否擁有私家車有關”;
的前提下認為“對限行的態度與是否擁有私家車有關”;
(2)為了了解限行之后是否對交通擁堵、環境染污起到改善作用,從上述調查的不贊同限行的人員中按是否擁有私家車分層抽樣抽取6人,再從這6人中隨機抽出3名進行電話回訪,求3人中至少有1人沒有私家車的概率.
附: 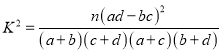 ,其中
,其中![]() .
.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某機構通過對某企業今年的生產經營情況的調查,得到每月利潤![]() (單位:萬元)與相應月份數
(單位:萬元)與相應月份數![]() 的部分數據如表:
的部分數據如表:
| 1 | 4 | 7 | 12 |
| 229 | 244 | 241 | 196 |
(1)根據如表數據,請從下列三個函數中選取一個恰當的函數描述![]() 與
與![]() 的變化關系,并說明理由,
的變化關系,并說明理由,![]() ,
,![]() ,
,![]() ;
;
(2)利用(1)中選擇的函數,估計月利潤最大的是第幾個月,并求出該月的利潤.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() :
:![]() 的左、右有頂點分別是
的左、右有頂點分別是![]() 、
、![]() ,上頂點是
,上頂點是![]() ,圓
,圓![]() :
:![]() 的圓心
的圓心![]() 到直線
到直線![]() 的距離是
的距離是![]() ,且橢圓的右焦點與拋物線
,且橢圓的右焦點與拋物線![]() 的焦點重合.
的焦點重合.
(Ⅰ)求橢圓![]() 的方程;
的方程;
(Ⅱ)平行于![]() 軸的動直線與橢圓和圓在第一象限內的交點分別為
軸的動直線與橢圓和圓在第一象限內的交點分別為![]() 、
、![]() ,直線
,直線![]() 、
、![]() 與
與![]() 軸的交點記為
軸的交點記為![]() ,
,![]() .試判斷
.試判斷![]() 是否為定值,若是,證明你的結論.若不是,舉反例說明.
是否為定值,若是,證明你的結論.若不是,舉反例說明.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com