【題目】在發生某公共衛生事件期間，有專業機構認為該事件在一段時間內沒有發生大規模群體感染的標志是“連續10天，每天新增疑似病例不超過7人”，根據過去10天甲、乙、丙、丁四地新增疑似病例數據，一定符合該標志的是( )
A. 甲地：總體均值為3，中位數為4
B. 乙地：總體均值為1，總體方差大于0
C. 丙地：總體均值為2，總體方差為3
D. 丁地：中位數為2，眾數為3
科目：高中數學 來源： 題型：
【題目】已知等差數列{an}的前n項和為Sn，等比數列{bn}的前n項和為Tn，a1=﹣1，b1=1，a2+b2=2．
（1）若a3+b3=5，求{bn}的通項公式；
（2）若T3=21，求S3．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖，
、
是離心率為
的橢圓
：
的左、右焦點，過作
軸的垂線交橢圓所得弦長為
，設
、
是橢圓上的兩個動點，線段
的中垂線與橢圓交于
、
兩點，線段的中點
的橫坐標為1.
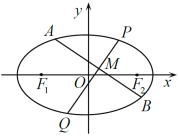
（1）求橢圓的方程；
（2）求
的取值范圍.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】設橢圓
:
的左右焦點分別為
，
，上頂點為
.
(Ⅰ)若
.
(i)求橢圓的離心率;
(ii)設直線
與橢圓的另一個交點為
，若
的面積為
，求橢圓的標準方程;
(Ⅱ)由橢圓上不同三點構成的三角形稱為橢圓的內接三角形，當
時，若以為直角頂點的橢圓的內接等腰直角三角形恰有3個，求實數
的取值范圍.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知橢圓
：
的離心率為
，橢圓
：
經過點
.
（1）求橢圓的標準方程；
（2）設點
是橢圓上的任意一點，射線
與橢圓交于點
，過點的直線
與橢圓有且只有一個公共點，直線與橢圓交于
，
兩個相異點，證明：
面積為定值.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某公司新發明了甲、乙兩種不同型號的手機，公司統計了消費者對這兩種型號手機的評分情況，作出如下的雷達圖，則下列說法不正確的是（ ）
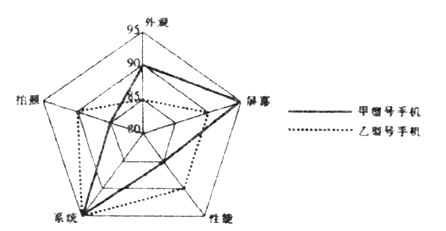
A. 甲型號手機在外觀方面比較好.B. 甲、乙兩型號的系統評分相同.
C. 甲型號手機在性能方面比較好.D. 乙型號手機在拍照方面比較好.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】為了引導居民合理用電，國家決定實行合理的階梯電價，居民用電原則上以住宅為單位（一套住宅為一戶）.
階梯級別 | 第一階梯 | 第二階梯 | 第三階梯 |
月用電范圍（度） | （0,210] | （210,400] |
|
某市隨機抽取10戶同一個月的用電情況，得到統計表如下：
居民用電戶編號 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
用電量（度） | 53 | 86 | 90 | 124 | 132 | 200 | 215 | 225 | 300 | 410 |
若規定第一階梯電價每度0.5元，第二階梯超出第一階梯的部分每度0.6元，第三階梯超出第二階梯的部分每度0.8元，試計算A居民用電戶用電410度時應電費多少元？
現要在這10戶家庭中任意選取3戶，求取到第二階梯電量的戶數的分布列與期望；
以表中抽到的10戶作為樣本估計全市的居民用電，現從全市中依次抽取10戶，若抽到
戶用電量為第一階梯的可能性最大，求
的值.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】隨著我國經濟的高速發展，汽車的銷量也快速增加，每年因道路交通安全事故造成傷亡人數超過
萬人，根據國家質量監督檢驗檢疫局發布的《車輛駕駛人員血液、呼氣酒精含量閥值與檢驗》（
-醉駕車的測試
）的規定：飲酒駕車是指車輛駕駛人員血液中的酒精含量大于或者等于
，小于
的駕駛行為；醉酒駕車是指車輛駕駛人員血液中的酒精含量大于或者等于的駕駛行為，某市交通部門從
年飲酒后駕駛機動車輛發生交通事故的駕駛員中隨機抽查了
人進行統計，得到如下數據：
酒精含量
|
|
|
|
|
|
發生交通事故的人數 |
|
|
|
|
|
已知從這人中任意抽取兩人，兩人均是醉酒駕車的概率是
.
（1）求
，
的值；
（2）實踐證明，駕駛人員血液中的酒精含量與發生交通事故的人數具有線性相關性，試建立
關于
的線性回歸方程；
（3）試預測，駕駛人員血液中的酒精含量為多少時，發生交通事故的人數會超過取樣人數的
？
參考數據：
，
回歸直線方程
中系數計算公式
，
.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
