
【題目】已知函數f(x)=3x,f(a+2)=27,函數g(x)=λ·2ax-4x的定義域為[0,2].
(1)求a的值;
(2)若函數g(x)在[0,2]上單調遞減,求λ的取值范圍;
(3)若函數g(x)的最大值是![]() ,求λ的值.
,求λ的值.
【答案】(1) a=1.
(2) (-∞,2].
(3) λ=![]() .
.
【解析】
(1)由指數的運算法則可得a=1.
(2)由(1)得g(x)=λ·2x-4x.由題意可知任取0≤x1<x2≤2,Δy=y2-y1<0,原問題等價于λ<![]() 對于x∈[0,2]恒成立.據此可得λ的取值范圍是(-∞,2].
對于x∈[0,2]恒成立.據此可得λ的取值范圍是(-∞,2].
(3)設t=2x,換元可知1≤t≤4.且y=-![]() ,1≤t≤4.結合二次函數的性質分類討論可得λ=
,1≤t≤4.結合二次函數的性質分類討論可得λ=![]() .
.
(1)27=3a+2=33,∴a=1.
(2)由(1)得,g(x)=λ·2x-4x.
任取0≤x1<x2≤2,則Δx=x2-x1>0,
∵g(x)在[0,2]上是減函數,
∴Δy=y2-y1<0,
Δy=y2-y1=g(x2)-g(x1)=λ·![]() -(λ·
-(λ·![]() )
)
=λ·![]() -(
-(![]() )2-[λ·
)2-[λ·![]() -(
-(![]() )2]
)2]
=(![]() )[λ-(
)[λ-(![]() )]<0,對于x∈[0,2]恒成立.
)]<0,對于x∈[0,2]恒成立.
∵![]() >0,
>0,
∴λ-(![]() )<0對于x∈[0,2]恒成立,
)<0對于x∈[0,2]恒成立,
即λ<![]() 對于x∈[0,2]恒成立.
對于x∈[0,2]恒成立.
∵![]() >2,
>2,
∴λ≤2.
∴λ的取值范圍是(-∞,2].
(3)設t=2x,∵0≤x≤2,
∴1≤2x≤4.
∴1≤t≤4.
y=-t2+λt=-![]() ,1≤t≤4.
,1≤t≤4.
①當![]() <1,即λ<2時,ymax=λ-1=
<1,即λ<2時,ymax=λ-1=![]() ,
,
∴λ=![]() ;
;
②當1≤![]() ≤4,即2≤λ≤8時,ymax=
≤4,即2≤λ≤8時,ymax=![]() ,
,
∴λ=![]() [2,8](舍);
[2,8](舍);
③當![]() >4,即λ>8時,ymax=-16+4λ=
>4,即λ>8時,ymax=-16+4λ=![]() ,
,
∴λ=![]() <8(舍).綜上λ=
<8(舍).綜上λ=![]() .
.


科目:高中數學 來源: 題型:
【題目】根據空氣質量指數API(為整數)的不同,可將空氣質量分級如下表:
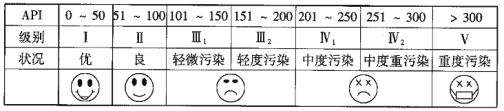
對某城市一年(365天)的空氣質量進行監測,獲得的API數據按照區間![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 進行分組,得到頻率分布條形圖如圖.
進行分組,得到頻率分布條形圖如圖.
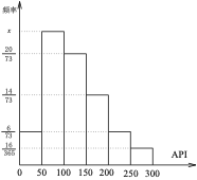
(1)求圖中![]() 的值;
的值;
(2)空氣質量狀況分別為輕微污染或輕度污染定為空氣質量Ⅲ級,求一年中空氣質量為Ⅲ級的天數
(3)小張到該城市出差一天,這天空氣質量為優良的概率是多少?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知二次函數f(x)的二次項系數為a(a<0).1,3是函數y=f(x)+2x的兩個零點.若方程f(x)+6a=0有兩個相等的根,求f(x)的解析式.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為回饋顧客,某商場擬通過摸球兌獎的方式對1000位顧客進行獎勵,規定:每位顧客從一個裝有4個標有面值的球的袋中一次性隨機摸出2個球,球上所標的面值之和為該顧客所獲的獎勵額.
(1)若袋中所裝的4個球中有1個所標的面值為50元,其余3個均為10元,求:
①顧客所獲的獎勵額為60元的概率;
②顧客所獲的獎勵額的分布列及數學期望;
(2)商場對獎勵總額的預算是60000元,并規定袋中的4個球只能由標有面值10元和50元的兩種球組成,或標有面值20元和40元的兩種球組成.為了使顧客得到的獎勵總額盡可能符合商場的預算且每位顧客所獲的獎勵額相對均衡,請對袋中的4個球的面值給出一個合適的設計,并說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】對于函數![]() ,若存在
,若存在![]() ,使
,使![]() 成立,則稱
成立,則稱![]() 為
為![]() 的不動點.已知函數
的不動點.已知函數![]()
![]() .
.
(1)當![]() ,
,![]() 時,求函數
時,求函數![]() 的不動點;
的不動點;
(2)若對任意實數![]() ,函數
,函數![]() 恒有兩個相異的不動點,求
恒有兩個相異的不動點,求![]() 的取值范圍;
的取值范圍;
(3)在(2)的條件下,若![]() 的兩個不動點為
的兩個不動點為![]() ,
,![]() ,且
,且![]() ,求實數
,求實數![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com