
【題目】設關于x的函數y=2cos2x-2acosx-(2a+1)的最小值為f(a),試確定滿足f(a)=![]() 的a的值,并求此時函數的最大值.
的a的值,并求此時函數的最大值.
【答案】5
【解析】
試題先化為二次函數形式,再根據對稱軸與定義區間位置關系確定最值取法,根據最小值為![]() ,解得a的值,代入最大值關系式可得最大值
,解得a的值,代入最大值關系式可得最大值
試題解析:解 令cosx=t,t∈[-1,1],
則y=2t2-2at-(2a+1)
=2(t-![]() )2-
)2-![]() -2a-1,
-2a-1,
關于t的二次函數的對稱軸是t=![]() ,
,
當![]() <-1,即a<-2時,
<-1,即a<-2時,
函數y在t∈[-1,1]上是單調遞增,
所以f(a)=f(-1)=1≠![]() ;
;
當![]() >1,即a>2時,
>1,即a>2時,
函數y在t∈[-1,1]上是單調遞減,
所以f(a)=f(1)=-4a+1=![]() ,
,
解得a=![]() ,這與a>2矛盾;
,這與a>2矛盾;
當-1≤![]() ≤1,即-2≤a≤2時,
≤1,即-2≤a≤2時,
f(a)=-![]() -2a-1=
-2a-1=![]() ,
,
即a2+4a+3=0,解得a=-1或a=-3,
因為-2≤a≤2,所以a=-1.
所以y=2t2+2t+1,t∈[-1,1],所以當t=1時,
函數取得最大值ymax=2+2+1=5.


 輕松奪冠全能掌控卷系列答案
輕松奪冠全能掌控卷系列答案科目:高中數學 來源: 題型:
【題目】一家保險公司決定對推銷員實行目標管理,即給推銷員確定一個具體的銷售目標,確定的銷售目標是否合適,直接影響到公司的經濟效益,如果目標定得過高,多數推銷員完不成任務,會使推銷員失去信心:如果目標定得太低,將不利于挖掘推銷員的工作潛力,下面一組數據是部分推銷員的月銷售額(單位:千元):
19.58 16.11 16.45 20.45 20.24 21.66 22.45 18.22 12.34
19.35 20.55 17.45 18.78 17.96 19.91 18.12 14.65 14.78
16.78 18.78 18.29 18.51 17.86 19.58 19.21 18.55 16.34
15.54 17.55 14.89 18.94 17.43 17.14 18.02 19.98 17.88
17.32 19.35 15.45 19.58 13.45 21.34 14.00 18.42 23.00
17.52 18.51 17.16 24.56 25.14
請根據這組樣本數據提出使65%的職工能夠完成銷售指標的建議.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】甲、乙、丙、丁、戊五位媽媽相約各帶一個小孩去觀看花卉展,她們選擇共享電動車出行,每輛電動車只能載兩人,其中孩子們表示都不坐自己媽媽的車,甲的小孩一定要坐戊媽媽的車,則她們坐車不同的搭配方式有( )
A. ![]() 種 B.
種 B. ![]() 種 C.
種 C. ![]() 種 D.
種 D. ![]() 種
種
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某創業團隊擬生產![]() 兩種產品,根據市場預測,
兩種產品,根據市場預測,![]() 產品的利潤與投資額成正比(如圖1),
產品的利潤與投資額成正比(如圖1),![]() 產品的利潤與投資額的算術平方根成正比(如圖2).(注: 利潤與投資額的單位均為萬元)
產品的利潤與投資額的算術平方根成正比(如圖2).(注: 利潤與投資額的單位均為萬元)

(注:利潤與投資額的單位均為萬元)
(1)分別將![]() 兩種產品的利潤
兩種產品的利潤![]() 、
、![]() 表示為投資額
表示為投資額![]() 的函數;
的函數;
(2)該團隊已籌集到10 萬元資金,并打算全部投入![]() 兩種產品的生產,問:當
兩種產品的生產,問:當![]() 產品的投資額為多少萬元時,生產
產品的投資額為多少萬元時,生產![]() 兩種產品能獲得最大利潤,最大利潤為多少?
兩種產品能獲得最大利潤,最大利潤為多少?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖所示的是某池塘中的浮萍蔓延的面積![]() 與時間
與時間![]() 月)的關系
月)的關系![]() 有以下敘述:
有以下敘述:
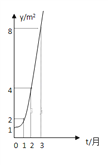
①這個指數函數的底數是2;
②第5個月時,浮萍的面積就會超過![]()
③浮萍從![]() 蔓延到
蔓延到![]() 需要經過1.5個月;
需要經過1.5個月;
④浮萍每個月增加的面積都相等;
⑤若浮萍蔓延到![]() 所經過的時間分別為
所經過的時間分別為![]() 則
則![]() .其中正確的是
.其中正確的是
A. ①② B. ①②③④ C. ②③④⑤ D. ①②⑤
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 的左、右焦點分別為
的左、右焦點分別為![]() 、
、![]() ,焦距為
,焦距為![]() ,直線
,直線![]() :
:![]() 與橢圓相交于
與橢圓相交于![]() 、
、![]() 兩點,
兩點,![]() 關于直線
關于直線![]() 的對稱點
的對稱點![]() 在橢圓上.斜率為
在橢圓上.斜率為![]() 的直線
的直線![]() 與線段
與線段![]() 相交于點
相交于點![]() ,與橢圓相交于
,與橢圓相交于![]() 、
、![]() 兩點.
兩點.

(1)求橢圓的標準方程;
(2)求四邊形![]() 面積的取值范圍.
面積的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓C:![]() ,直線l:y=kx+b與橢圓C相交于A、B兩點.
,直線l:y=kx+b與橢圓C相交于A、B兩點.
(1)如果k+b=﹣![]() ,求動直線l所過的定點;
,求動直線l所過的定點;
(2)記橢圓C的上頂點為D,如果∠ADB=![]() ,證明動直線l過定點P(0,﹣
,證明動直線l過定點P(0,﹣![]() );
);
(3)如果b=﹣![]() ,點B關于y軸的對稱點為B
,點B關于y軸的對稱點為B![]() ,向直線AB
,向直線AB![]() 是過定點?如果是,求出定點的坐標;如果不是,請說明理由.
是過定點?如果是,求出定點的坐標;如果不是,請說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com