【題目】已知函數
.
（1）求
在點
處的切線方程；
（2）當
時，證明：
；
（3）判斷曲線
與
是否存在公切線，若存在，說明有幾條，若不存在，說明理由.
【答案】（1）
；（2）證明見解析；（3）存在；存在2條公切線
【解析】
（1）計算
，根據曲線在該點處導數的幾何意義可得切線的斜率，然后計算
，利用點斜式，可得結果.
（2）分別構造
，通過導數研究
的性質，可得 
，
，簡單判斷，可得結果.
（3）分別假設
與
的切線，根據公切線，可得
，利用導數研究函數
零點個數，根據
性質可得結果.
解：（1）
的定義域
又
所以
在點
處的切線方程為：.
（2）設
，
，
|
|
|
|
|
|
|
|
| ↑ | 極大值 | ↓ |
設
則
在
上恒成立
綜上
（3）曲線與存在公切線，且有2條，理由如下：
由（2）知曲線與無公共點，
設
分別切曲線與于
，則
，
若
，即曲線與有公切線，則
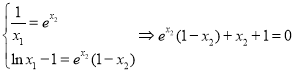
令，
則曲線與有公切線，當且僅當有零點，
，
當
時，
，在
單調遞增，
當
時，
，
在
單調遞減
，
所以存在
，使得
且當
時，
單調遞增，
當
時，
單調遞減
，
又
所以在
內各存在有一個零點
故曲線與存在2條公切線.
科目：高中數學 來源： 題型：
【題目】如圖所示的曲線圖是2020年1月25日至2020年2月12日陜西省及西安市新冠肺炎累計確診病例的曲線圖，則下列判斷正確的是（ ）
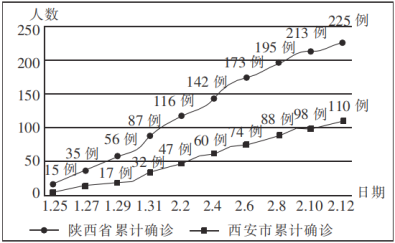
A.1月31日陜西省新冠肺炎累計確診病例中西安市占比超過了
B.1月25日至2月12日陜西省及西安市新冠肺炎累計確診病例都呈遞增趨勢
C.2月2日后到2月10日陜西省新冠肺炎累計確診病例增加了97例
D.2月8日到2月10日西安市新冠肺炎累計確診病例的增長率大于2月6日到2月8日的增長率
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某險種的基本保費為a(單位：元)，繼續購買該險種的投保人稱為續保人，續保人本年度的保費與其上年度出險次數的關聯如下：
上年度出險次數 | 0 | 1 | 2 | 3 | 4 | ≥5 |
保費 | 0.85a | a | 1.25a | 1.5a | 1.75a | 2a |
隨機調查了該險種的200名續保人在一年內的出險情況，得到如下統計表：
出險次數 | 0 | 1 | 2 | 3 | 4 | ≥5 |
頻數 | 60 | 50 | 30 | 30 | 20 | 10 |
(1)記A為事件：“一續保人本年度的保費不高于基本保費”，求P(A)的估計值；
(2)記B為事件：“一續保人本年度的保費高于基本保費但不高于基本保費的160%”，求P(B)的估計值；
(3)求續保人本年度平均保費的估計值．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖所示，在四棱錐
中，四邊形
為矩形，
為等腰三角形，
，平面
平面，且
，
，
，
分別為
，
的中點.
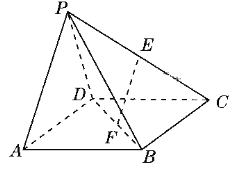
（1）證明：
平面
；
（2）證明：平面
平面；
（3）求四棱錐的體積.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某苗木基地常年供應多種規格的優質樹苗.為更好地銷售樹苗，建設生態文明家鄉和美好家園，基地積極主動地聯系了甲、乙、丙三家公司，假定基地得到公司甲、乙、丙的購買合同的概率分別
、
、
，且基地是否得到三家公司的購買合同是相互獨立的.
（1）若公司甲計劃與基地簽訂300棵銀杏實生苗的銷售合同，每棵銀杏實生苗的價格為90元，栽種后，每棵樹苗當年的成活率都為0.9，對當年沒有成活的樹苗，第二年需再補種1棵.現公司甲為苗木基地提供了兩種售后方案，
方案一：公司甲購買300棵銀杏樹苗后，基地需提供一年一次，共計兩年的補種服務，且每次補種人工及運輸費用平均為800元；
方案二：公司甲購買300棵銀杏樹苗后，基地一次性地多給公司甲60棵樹苗，后期的移栽培育工作由公司甲自行負責.
若基地首次運送方案一的300棵樹苗及方案二的360棵樹苗的運費及栽種費用合計都為1600元，試估算兩種方案下苗木基地的合同收益分別是多少？
（2）記
為該基地得到三家公司購買合同的個數，若
，求隨機變量的分布列與數學期望
.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
