
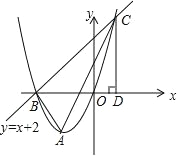
【題目】如圖,已知拋物線 y=x2+2x 的頂點為 A,直線 y=x+2 與拋物線交于 B,C 兩點.
(1)求 A,B,C 三點的坐標;
(2)作 CD⊥x 軸于點 D,求證:△ODC∽△ABC;
(3)若點 P 為拋物線上的一個動點,過點 P 作 PM⊥x 軸于點 M,則是否還存在除 C 點外的其他位置的點,使以 O,P,M 為頂點的三角形與△ABC 相似? 若存在,請求出這樣的 P 點坐標;若不存在,請說明理由.
【答案】(1)B(﹣2,0),C(1,3);(2)見解析;(3)存在這樣的點 P,坐標為(﹣![]() ,﹣
,﹣![]() )或(﹣
)或(﹣![]() ,
,![]() )或(﹣5,15).
)或(﹣5,15).
【解析】
(1)可設頂點式,把原點坐標代入可求得拋物線解析式,聯立直線與拋物線解析式,可求得C點坐標;
(2)根據勾股定理可得∠ABC=90°,進而可求△ODC∽△ABC.
(3)設出p點坐標,可表示出M點坐標,利用三角形相似可求得p點的坐標.
(1)解:y=x2+2x=(x+1)2﹣1,
∴頂點 A(﹣1,﹣1);
由 ![]() ,解得:
,解得:![]() 或
或![]()
∴B(﹣2,0),C(1,3);
(2)證明:∵A(﹣1,﹣1),B(﹣2,0),C(1,3),
∴AB=![]() ,
,
BC= ![]() ,
,
AC=![]() ,
,
∴AB2+BC2=AC2,![]() ,
,
∴∠ABC=90°,
∵OD=1,CD=3,
∴![]() =
=![]() ,
,
∴![]() ,∠ABC=∠ODC=90°,
,∠ABC=∠ODC=90°,
∴△ODC∽△ABC;
(3)存在這樣的 P 點,設 M(x,0),則 P(x,x2+2x),
∴OM=|x|,PM=|x2+2x|,
當以 O,P,M 為頂點的三角形與△ABC 相似時,
有![]() 或
或 ![]() ,
,
由(2)知:AB= ![]() ,CB=
,CB=![]() ,
,
①當![]() 時,則
時,則 ![]() =
=![]() , 當 P 在第二象限時,x<0,x2+2x>0,
, 當 P 在第二象限時,x<0,x2+2x>0,
∴![]() ,解得:x1=0(舍),x2= -
,解得:x1=0(舍),x2= -![]() , 當 P 在第三象限時,x<0,x2+2x<0,
, 當 P 在第三象限時,x<0,x2+2x<0,
∴![]() =
= ![]() ,解得:x1=0(舍),x2=-
,解得:x1=0(舍),x2=-![]() ,
,
②當![]() 時,則
時,則 ![]() =3, 同理代入可得:x=﹣5 或 x=1(舍),
=3, 同理代入可得:x=﹣5 或 x=1(舍),
綜上所述,存在這樣的點 P,坐標為(-![]() ,-
,-![]() )或(-
)或(-![]() ,
,![]() )或(﹣5,15).
)或(﹣5,15).


 天天練口算系列答案
天天練口算系列答案科目:初中數學 來源: 題型:
【題目】已知:如圖,在Rt△ABC中,∠C=90°,AB=5cm,AC=3cm,動點P從點B出發沿射線BC以1cm/s的速度移動,設運動的時間為t秒.

(1)求BC邊的長;
(2)當△ABP為直角三角形時,求t的值;
(3)當△ABP為等腰三角形時,求t的值
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】直線y=![]() x+4與x軸、y軸分別交于點A和點B,點C,D分別為線段AB,OB的中點,點P為OA上一動點,PC+PD值最小時點P的坐標為.
x+4與x軸、y軸分別交于點A和點B,點C,D分別為線段AB,OB的中點,點P為OA上一動點,PC+PD值最小時點P的坐標為.

A. (-3,0) B. (-6,0) C. (-![]() ,0) D. (-
,0) D. (-![]() ,0)
,0)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,矩形ABCD中,對角線AC,BD相交于點O,∠ADB=30°,E為BC邊上一點,∠AEB=45°,CF⊥BD于F.下列結論:①BE=CD,②BF=3DF,③AE=![]() AO,④CE=CF.正確的結論有( )
AO,④CE=CF.正確的結論有( )
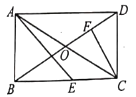
A. ①②B. ②③C. ①②④D. ①②③
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】以下是八(1)班學生身高的統計表和扇形統計圖,請回答以下問題.
八(1)班學生身高統計表
組別 | 身高(單位:米) | 人數 |
第一組 | 1.85以上 | 1 |
第二組 |
| |
第三組 |
| 19 |
第四組 |
| |
第五組 | 1.55以下 | 8 |
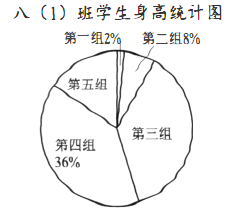
(1)求出統計表和統計圖缺的數據.
(2)八(1)班學生身高這組數據的中位數落在第幾組?
(3)如果現在八(1)班學生的平均身高是1.63 ![]() ,已確定新學期班級轉來兩名新同學,新同學的身高分別是1.54
,已確定新學期班級轉來兩名新同學,新同學的身高分別是1.54 ![]() 和1.77
和1.77 ![]() ,那么這組新數據的中位數落在第幾組?
,那么這組新數據的中位數落在第幾組?
查看答案和解析>>
科目:初中數學 來源: 題型:
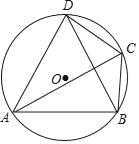
【題目】如圖,在⊙O的內接四邊形ABCD中,∠BCD=120°,CA平分∠BCD.
(1)求證:△ABD是等邊三角形;
(2)若BD=3,求⊙O的半徑.
查看答案和解析>>
科目:初中數學 來源: 題型:
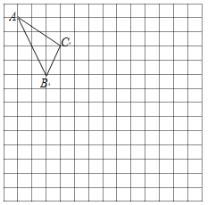
【題目】如圖,在正方形網格中,每一個小正方形的邊長為1.△ABC的三個頂點都在格點上,A、C的坐標分別是(﹣4,6),(﹣1,4).
(1)請在圖中的網格平面內建立平面直角坐標系;
(2)請畫出△ABC向右平移6個單位的△A1B1C1,并寫出C1的坐標 ;
(3)請畫出△ABC關于原點O對稱的△A2B2C2 , 并寫出點C2的坐標 .
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在直角坐標系中,正方形OABC的頂點O與原點重合,頂點A、C分別在x軸、y軸上,反比例函數y=![]() (k≠0,x>0)的圖象與正方形的兩邊AB、BC分別交于點E、F,FD⊥x軸,垂足為D,連接OE、OF、EF,FD與OE相交于點G.下列結論:①OF=OE;②∠EOF=60°;③四邊形AEGD與△FOG面積相等;④EF=CF+AE;⑤若∠EOF=45°,EF=4,則直線FE的函數解析式為
(k≠0,x>0)的圖象與正方形的兩邊AB、BC分別交于點E、F,FD⊥x軸,垂足為D,連接OE、OF、EF,FD與OE相交于點G.下列結論:①OF=OE;②∠EOF=60°;③四邊形AEGD與△FOG面積相等;④EF=CF+AE;⑤若∠EOF=45°,EF=4,則直線FE的函數解析式為![]() .其中正確結論的個數是( )
.其中正確結論的個數是( )
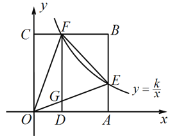
A.2B.3C.4D.5
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com