【題目】如圖，Rt△AOB的斜邊AB切⊙O于點C，OA交⊙O于點D，連接DC并延長交OB的延長線于點E．已知∠A=∠E，若AB=6，則BC的長為__________．
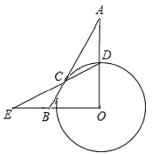
【答案】1.5
【解析】
由AB與⊙相切于C可得：OC⊥AB，可證得∠A=∠COE=∠E=x，利用三角形內角和即可求出x=30，利用30°的直角三角形的性質可得：BO=3及BC=1.5．
連接OC
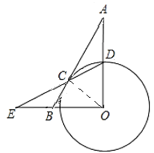
∵AB與⊙相切于C
∴OC⊥AB
∴∠ABO+∠COB=90°，∠A+∠ABO=90°
∴∠A=∠COE
∵∠A=∠E
∴∠E=∠COE=∠A =x
∴在△ECO中，∠DCO=∠E+∠COE=2x
∵OC=OD
∴∠EDO=∠DCO=2x
在Rt△EOD中，∠E+∠EDO=90°
∴x+2x=90°
∴x=30°
在Rt△ABO中，∠A=30°，AB=6
∴BO=3
在Rt△BCO中，∠COB=30°，BO=3
∴BC=1.5
故答案為：1.5
科目：初中數學 來源： 題型：
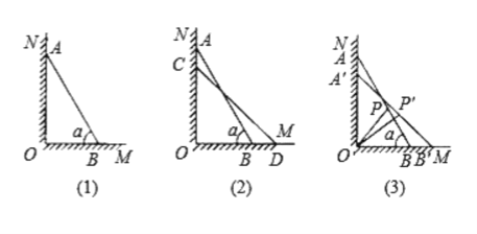
【題目】如圖（1）所示，一架長
米的梯子
斜靠在與地面
垂直的墻壁
上，梯子與地面所成的角
為
度.
（1）求圖（1）中的
與
的長度;
（2）若梯子頂端
沿
下滑，同時底端
沿向右滑行.
①如圖（2）所示，設點下滑到
點，點向右滑行到
點，并且
，請計算
的長度;
②如圖（3）所示，當點下滑到
，點向右滑行到
點時，梯子的中點
也隨之運動到
點，若
，試求
的長度.
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】有這樣一個問題探究函數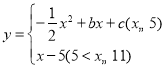
（b、c為常數）的圖象和性質．元元根據學習函數的經驗，對該函數的圖象和性質進行了以下探究：
下面是元元的探究過程，請你補充完整
x | …… | ﹣1 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | …… |
y | …… | 0 | 2.5 | 4 | m | 4 | 2.5 | 0 | 1 | …… |
（1）根據上表信息，其中b＝____，c＝_____，m＝______．
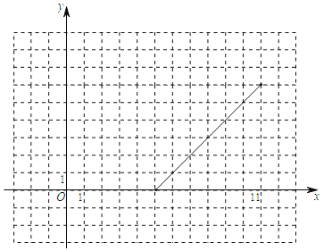
（2）如圖，在下面平面直角坐標系中，描出以補全后的表中各對應值為坐標的點，并畫出該函數的另一部分圖象；
（3）觀察函數圖象，請寫出該函數的一條性質：______．
（4）解決問題：若直線y＝3n+2（n為常數）與該函數圖象有3個交點時，求n的范圍．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】1400多年前，我國隋代建造的石拱橋——趙州橋(如圖(1))，是我國古代人民勤勞與智慧的結晶．如圖(2)是它的簡化示意圖，主橋拱是
，拱高(的中點到弦
的距離)為
．
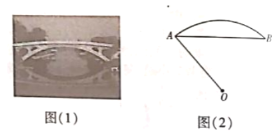
（1）在圖(2)中(點
為圓心)，用尺規作圖作出的中點
．(不要求寫作法，但保留作圖痕跡)
（2）若
，求主橋拱的跨度的長．(結果精確到
參考數據：
)
查看答案和解析>>
科目：初中數學 來源： 題型：
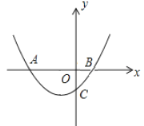
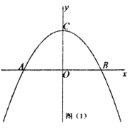
【題目】如圖，已知拋物線
交x軸于A(－4，0)，B兩點，交y軸于點C(0，－2)．
（1）求拋物線的解析式；
（2）過點M(m，0)(－4＜m＜0)且垂直于x軸的直線與拋物線相交于點N，求線段OM＋MN的最大值．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】在△ABC中，∠ABC＝2∠ACB，BD平分∠ABC交AC于點D．
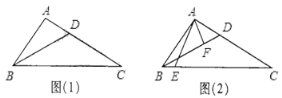
（1）如圖（1），若AB＝3，AC＝5，求AD的長；
（2）如圖（2），過點A分別作AC，BD的垂線，分別交BC，BD于點E，F．
①求證：∠ABC＝∠EAF；
②求
的值．
查看答案和解析>>
科目：初中數學 來源： 題型：
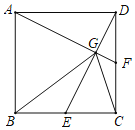
【題目】如圖，正方形ABCD中，E、F分別為BC、CD的中點，AF與DE交與點G．則下列結論中：①AF⊥DE；②AD＝BG；③GE+GF＝
GC；④S△AGB＝2S四邊形ECFG．其中正確的是（ ）
A.1個B.2個C.3個D.4個
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，拋物線
交
軸于
、
（左右）兩點，交
軸于點
，且
．
（1）如圖（1）求拋物線的解析式；
（2）如圖（2）
為第四象限拋物線上一點，連接
，將線段沿著軸翻折，得到線段
，連接
，設點的橫坐標為
，
的面積為
，求與的函數關系式；
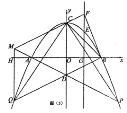
（3）如圖（3）在（2）的條件下，
是第一象限拋物線上的一點，
軸交
的延長線于
，垂足是
，過點作
軸交軸于
、交直線
于點
，連接
，
，求點的坐標．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
