
【題目】如圖,已知正方形ABCD的邊長為4,以AB為一邊作等邊△ABE,使點E落在正方形ABCD的內部,連接AC交BE于點F,連接CE、DE,則下列說法中:①△ADE≌△BCE;②∠ACE=30°;③AF=![]() CF;④
CF;④ ![]() =2+
=2+![]() ,其中正確的有( )
,其中正確的有( )

A. 1個 B. 2個 C. 3個 D. 4個
【答案】D
【解析】
根據正方形的性質,全等三角形的判定,可以證明①②正確,作FH⊥BC于H,設FH=CH=a,則BH=![]() a,利用勾股定理求出a,即可判斷③④正確;
a,利用勾股定理求出a,即可判斷③④正確;
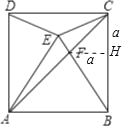
∵四邊形ABCD是正方形,△AEB是等邊三角形,
∴AD=AE=AB=BE=BC,∠DAB=∠CBA=90°,∠EAB=∠EBA=60°,
∴∠DAE=∠EBC=30°,
∴△ADE≌△BCE,故①正確,
∵∠BEC=∠BCE=![]() (180°30°)=75°,∠ACB=45°,
(180°30°)=75°,∠ACB=45°,
∴∠ACE=∠BCE∠ACB=30°,故②正確,
作FH⊥BC于H,設FH=CH=a,則BH=3![]() ,
,
∵BC=4,
∴a+![]() a=4,
a=4,
∴a=2![]() 2,
2,
∴CF=![]() a=2
a=2![]() 2
2![]() ,
,
∵AC=4![]() ,
,
∴AF=AC=CF=6![]() 2
2![]() ,
,
∴AF=![]() CF,故③正確,
CF,故③正確,
∵BF=2FH=4![]() 4,
4,
∴EF=BEBF=84![]() ,
,
∴S△BCES△ECF=![]() =2+
=2+![]() ,故④正確,
,故④正確,
故選:D.


 陽光試卷單元測試卷系列答案
陽光試卷單元測試卷系列答案科目:初中數學 來源: 題型:
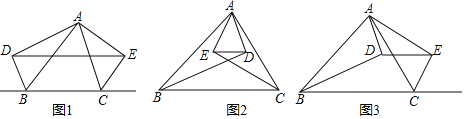
【題目】已知,△ABC,AD⊥BD于點D,AE⊥CE于點E,連接DE.
(1)如圖1,若BD,CE分別為△ABC的外角平分線,求證:DE=![]() (AB+BC+AC).
(AB+BC+AC).
(2)如圖2,若BD,CE分別為△ABC的內角平分線,(1)中的結論成立嗎?若成立請說明理由;若不成立,請猜想出新的結論并證明;
(3)如圖3,若BD,CE分別為△ABC的一個內角和一個外角的平分線,AB=8,BC=10,AC=7,請直接寫出DE的長為______.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在長方形![]() 中,邊
中,邊![]() ,
,![]() ,以點
,以點![]() 為原點,
為原點,![]() ,
,![]() 所在的直線為
所在的直線為![]() 軸和
軸和![]() 軸,建立直角坐標系.
軸,建立直角坐標系.
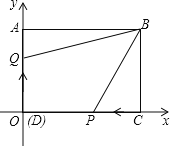
(1)點![]() 的坐標為
的坐標為![]() ,則
,則![]() 點坐標為______,
點坐標為______,![]() 點坐標為______;
點坐標為______;
(2)當點![]() 從
從![]() 出發,以2單位/秒的速度沿
出發,以2單位/秒的速度沿![]() 方向移動(不過
方向移動(不過![]() 點),
點),![]() 從原點
從原點![]() 出發以1單位/秒的速度沿
出發以1單位/秒的速度沿![]() 方向移動(不過
方向移動(不過![]() 點),
點),![]() ,
,![]() 同時出發,在移動過程中,四邊形
同時出發,在移動過程中,四邊形![]() 的面積是否變化?若不變,求其值;若變化,求其變化范圍.
的面積是否變化?若不變,求其值;若變化,求其變化范圍.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,高速公路上有A、B兩點相距25km,C、D為兩村莊,已知DA=10km,CB=15km.DA⊥AB于A,CB⊥AB于B,現要在AB上建一個服務站E,使得C、D兩村莊到E站的距離相等,則AE的長是( )km.

A.5B.10C.15D.25
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,△ABC中,AB=AC,AD是△ABC的角平分線,點O為AB的中點,連接DO并延長到點E,使OE=OD,連接AE,BE.

(1)求證:四邊形AEBD是矩形;
(2)當△ABC滿足什么條件時,矩形AEBD是正方形,并說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】閱讀下面材料:
如圖![]() ,把
,把![]() 沿直線
沿直線![]() 平行移動線段
平行移動線段![]() 的長度,可以變到
的長度,可以變到![]() 的位置;
的位置;
如圖![]() ,以
,以![]() 為軸,把
為軸,把![]() 翻折
翻折![]() ,可以變到
,可以變到![]() 的位置;
的位置;
如圖![]() ,以點
,以點![]() 為中心,把
為中心,把![]() 旋轉
旋轉![]() ,可以變到
,可以變到![]() 的位置.
的位置.
像這樣,其中一個三角形是由另一個三角形按平行移動、翻折、旋轉等方法變成的.這種只改變位置,不改變形狀大小的圖形變換,叫做三角形的全等變換.
回答下列問題:
①在圖![]() 中,可以通過平行移動、翻折、旋轉中的哪一種方法怎樣變化,使
中,可以通過平行移動、翻折、旋轉中的哪一種方法怎樣變化,使![]() 變到
變到![]() 的位置;
的位置;
②指圖中線段![]() 與
與![]() 之間的關系,為什么?
之間的關系,為什么?

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在⊙O中,將![]() 沿弦BC所在直線折疊,折疊后的弧與直徑AB相交于點D,連接CD.
沿弦BC所在直線折疊,折疊后的弧與直徑AB相交于點D,連接CD.
(1)若點D恰好與點O重合,則∠ABC= °;
(2)延長CD交⊙O于點M,連接BM.猜想∠ABC與∠ABM的數量關系,并說明理由.

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com