
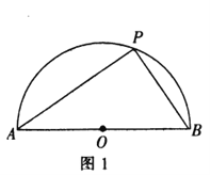
【題目】[問題發現]如圖1,半圓![]() 的直徑
的直徑![]() 是半圓
是半圓![]() 上的一個動點,則
上的一個動點,則![]() 面積的最大值是_.
面積的最大值是_.
[問題解決]如圖2所示的是某街心花園的一角.在扇形![]() 中,
中,![]() 米,在圍墻
米,在圍墻![]() 和
和![]() 上分別有兩個入口
上分別有兩個入口![]() 和
和![]() 且
且![]() 米,
米,![]() 是
是![]() 的中點,出口
的中點,出口![]() 在
在![]() 上.現準備沿
上.現準備沿![]() 從入口到出口鋪設兩條景觀小路,在四邊形
從入口到出口鋪設兩條景觀小路,在四邊形![]() 內種花,在剩余區域種草.
內種花,在剩余區域種草.
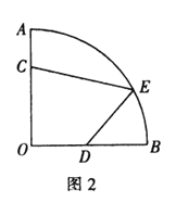
①出口![]() 設在距直線
設在距直線![]() 多遠處可以使四邊形
多遠處可以使四邊形![]() 的面積最大?最大面積是多少?(小路寬度不計)
的面積最大?最大面積是多少?(小路寬度不計)
②已知鋪設小路![]() 所用的普通石材每米的造價是
所用的普通石材每米的造價是![]() 元,鋪設小路
元,鋪設小路![]() 所用的景觀石材每米的造價是
所用的景觀石材每米的造價是![]() 元問:在
元問:在![]() 上是否存在點
上是否存在點![]() ,使鋪設小路
,使鋪設小路![]() 和
和![]() 的總造價最低?若存在,請求出最低總造價和出口
的總造價最低?若存在,請求出最低總造價和出口![]() 距直線
距直線![]() 的距離;若不存在,請說明理由.
的距離;若不存在,請說明理由.
【答案】[問題發現]25;[問題解決]①出口![]() 設在距直線
設在距直線![]() 米處可以使四邊形
米處可以使四邊形![]() 的面積最大,最大為
的面積最大,最大為![]() 平方米;②總造價的最小值為
平方米;②總造價的最小值為![]() 元,出口
元,出口![]() 距直線
距直線![]() 的距離為
的距離為![]() 米
米
【解析】
[問題發現]![]() 的底邊一定,面積最大也就是P點到AB的距離最大,故當
的底邊一定,面積最大也就是P點到AB的距離最大,故當![]() 時底邊
時底邊![]() 上的高最大,再計算此時
上的高最大,再計算此時![]() 面積即可.
面積即可.
[問題解決]①根據四邊形CODE面積=![]() ,求出
,求出![]() 最大時即可,然后作
最大時即可,然后作![]() ,證明
,證明![]() ,利用相似三角形的性質求出
,利用相似三角形的性質求出![]() 即可;
即可;
②先利用相似三角形將費用問題轉化為CE+2DE=CE+QE,求CE+QE的最小值問題,然后利用相似三角形性質和勾股定理求解即可.
解:[問題發現]:
如圖1,點![]() 運動至半圓
運動至半圓![]() 的中點時,底邊
的中點時,底邊![]() 上的高最大,即
上的高最大,即![]()
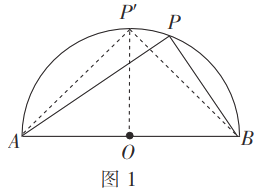
此時![]() 的面積最大,最大值為
的面積最大,最大值為![]() ;
;
[問題解決]![]() 如圖2,連接
如圖2,連接![]() 作
作![]() ,垂足為
,垂足為![]() 延長
延長![]() 交
交![]() 于點
于點![]() ,
,
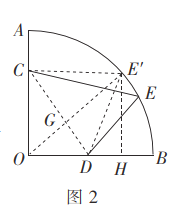
則此時![]() 的面積最大.
的面積最大.
![]() 為
為![]() 的中點,
的中點,
![]() ,
,
在![]() 中,
中,![]() ,
,
![]() ,
,
![]() 四邊形
四邊形![]() 面積的最大值為
面積的最大值為![]() ,
,
作![]() 垂足為
垂足為![]() ,
,
![]()
![]() .
.
又![]() ,
,
![]() ,
,
![]()
![]()
![]() ,
,
![]() 出口
出口![]() 設在距直線
設在距直線![]() 米處可以使四邊形
米處可以使四邊形![]() 的面積最大,最大為
的面積最大,最大為![]() 平方米;
平方米;
![]() 鋪設小路
鋪設小路![]() 和
和![]() 的總造價為
的總造價為![]()
如圖3,連接![]() 延長
延長![]() 到點
到點![]() 使
使![]() ,連接
,連接![]()
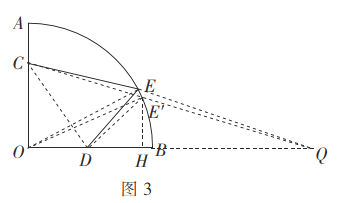
在![]() 與
與![]() 中,
中,![]() ,且
,且![]() ,
,
![]()
故![]()
![]() ,問題轉化為求
,問題轉化為求![]() 的最小值,
的最小值,
連接![]() 交
交![]() 于點
于點![]() ,
,
此時![]() 取得最小值為
取得最小值為![]() .
.
在![]() 中,
中,![]() ,
,
![]() ,
,
故總造價的最小值為![]() 元,
元,
作![]() 垂足為
垂足為![]() ,連接
,連接![]() .
.
設![]() 則
則![]() .
.
在![]() 中,
中,![]() ,
,
![]()
解得![]() ,
,![]() (舍去),
(舍去),
![]() 總造價的最小值為
總造價的最小值為![]() 元,出口
元,出口![]() 距直線
距直線![]() 的距離為
的距離為![]() 米.
米.


科目:初中數學 來源: 題型:
【題目】楊華與季紅用5張同樣規格的硬紙片做拼圖游戲,正面如圖1所示,背面完全一樣,將它們背面朝上攪勻后,同時抽出兩張.規則如下:當兩張硬紙片上的圖形可拼成電燈或小人時,楊華得1分;當兩張硬紙片上的圖形可拼成房子或小山時,季紅得1分(如圖2).問題:游戲規則對雙方公平嗎?請說明理由;若你認為不公平,如何修改游戲規則才能使游戲對雙方公平?

查看答案和解析>>
科目:初中數學 來源: 題型:
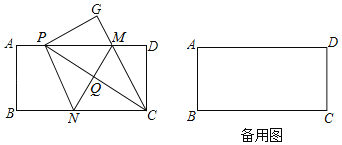
【題目】如圖,現有一張矩形紙片ABCD,AB=4,BC=8,點M,N分別在矩形的邊AD,BC上,將矩形紙片沿直線MN折疊,使點C落在矩形的邊AD上,記為點P,點D落在G處,連接PC,交MN丁點Q,連接CM.
(1)求證:PM=PN;
(2)當P,A重合時,求MN的值;
(3)若△PQM的面積為S,求S的取值范圍.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,以![]() 為頂點的拋物線
為頂點的拋物線![]() 交
交![]() 軸于點
軸于點![]() ,
,![]() ,交
,交![]() 軸于點
軸于點![]() .
.
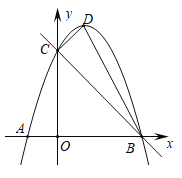
(1)求拋物線的解析式;
(2)在直線![]() 上有一點
上有一點![]() ,使
,使![]() 的值最小,求點
的值最小,求點![]() 的坐標;
的坐標;
(3)在![]() 軸上是否存在一點
軸上是否存在一點![]() ,使得以
,使得以![]() ,
,![]() ,
,![]() 為頂點的三角形與
為頂點的三角形與![]() 相似?若存在,請求出點
相似?若存在,請求出點![]() 的坐標;若不存在,請說明理由.
的坐標;若不存在,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知△ABC是⊙O的內接三角形,∠BAC的平分線交⊙O于點D.
(I)如圖①,若BC是⊙O的直徑,BC=4,求BD的長;
(Ⅱ)如圖②,若∠ABC的平分線交AD于點E,求證:DE=DB.
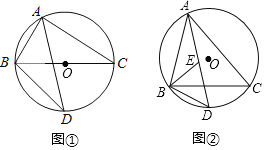
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某校開展主題為“垃圾分類,綠色生活新時尚”的宣傳活動,為了解學生對垃圾分類知識的掌握情況,學生會隨機抽取了20名七、八年級學生(每個年級各10人)進行問卷調查,并把他們的得分繪制成了如下表格,計分采用10分制(得分均取整數)成績達到6分或6分以上為及格,達到9分及以上為優秀,成績如表1所示,并制作了成績分析表(表2).
表1
七年級 | 5 | 8 | 8 |
| 8 | 10 | 10 | 8 | 5 | 5 |
八年級 | 10 | 6 | 6 | 9 |
| 4 | 5 | 7 | 10 | 8 |
表2
年級 | 平均數 | 中位數 | 眾數 | 方差 | 及格率 | 優秀率 |
七年級 | 7.6 | 8 | 8 | 3.82 | 70% |
|
八年級 | 7.5 |
| 10 | 4.94 | 80% | 40% |
(1)在表1中,![]() _____,
_____,![]() _____;在表2中,
_____;在表2中,![]() _____,
_____,![]() ______;
______;
(2)根據表2成績數據分析,你認為哪個年級的學生對垃圾分類了解更加深入,請說明你的理由;
(3)小明根據表2數據作出如下判斷:
①七年級學生成績的平均數高于八年級,故七年級學生一定比八年級學生優秀;
②被調查對象中,七年級學生的成績更加穩定;
③學校七年級和八年級共有400人,估計有280人成績達到優秀;
④七年級不及格人數比八年級多;
對小明的四個結論,隨機任選兩個,求都是錯誤的概率.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】隨著通訊技術的迅猛發展,人與人之間的溝通方式更多樣、便捷某校數學興趣小組設計了“你最喜歡的溝通方式”調查問卷(每人必選且只選一種),在全校范圍內隨機調查了部分學生,將統計結果繪制了如下兩幅不完整的統計圖,請結合圖中所給的信息解答下列問題:
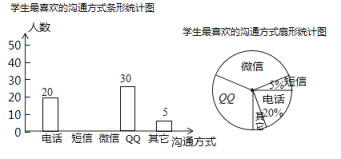
(1)這次統計共抽查了多少名學生?在扇形統計圖中,表示" ![]() "的扇形圓心角的度數是多少;
"的扇形圓心角的度數是多少;
(2)將條形統計圖補充完整;
(3)該校共有1500名學生,請估計該校最喜歡用 “微信”進行溝通的學生大約有多少名?
(4)某天甲、乙兩名同學都想從“微信"、"![]() "、“電話"三種溝通方式中選一種方式與對方聯系,請用列表或畫樹狀圖的方法求出甲、乙兩名同學恰好選擇同一種溝通方式的概率.
"、“電話"三種溝通方式中選一種方式與對方聯系,請用列表或畫樹狀圖的方法求出甲、乙兩名同學恰好選擇同一種溝通方式的概率.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,△ABC中,∠BAC=45°,∠ACB=30°,將△ABC繞點A順時針旋轉得到△AB1C1,當點C1、B1、C三點共線時,旋轉角為α,連接BB1,交AC于點D.下列結論:①△AC1C為等腰三角形;②△AB1D∽△BCD;③α=75°;④CA=CB1,其中正確的是( )
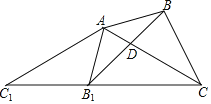
A.①③④B.①②④C.②③④D.①②③④
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com